\require{AMSmath}

Mantel afgeknotte kegel

Graag zou ik willen weten hoe het volgende werkt:

Ik heb een afgeknotte kegel met hoogte 135 mm, bovendiameter 85, onderdiameter 65 mm. Hier moet een sleeve/mantel omheen met een hoogte van 105mm, en deze moet in het midden om de afgeknotte kegel heen sluiten.

Ik vermoed dat de s, r en $\theta $ van de afgeknotte kegel berekenen helpt bij het maken van de uitslag van de sleeve/mantel, maar ik kom niet verder met het doorrekenen naar hoogte-aanpassingen, omdat dan de diameters veranderen.

Student universiteit - donderdag 4 januari 2024

Antwoord

Bekijk het volgende plaatje

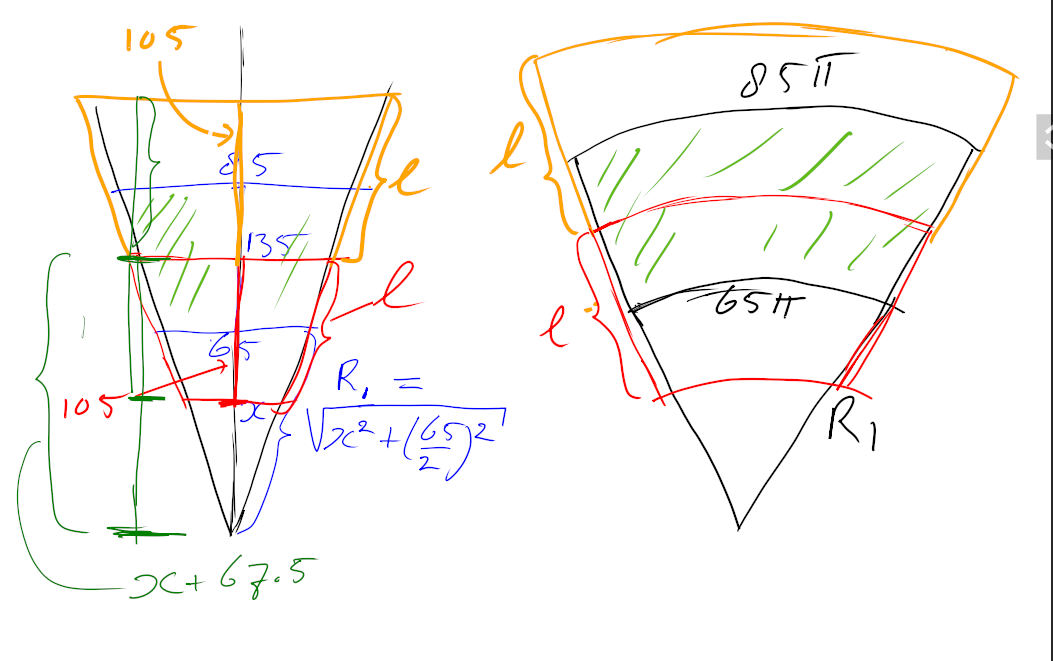
Daarin heb ik (schematisch) de afgeknotte kegel getekend en ik heb hem volledig gemaakt tot de top. Het getal $x$ is de hoogte van het toegevoegde stuk. Wegens gelijkvormigheid moet gelden dat $x:65 = (x+135):85$, daaruit leidt je af dat $x=438.75$ (alles in $\mathrm{mm}$ natuurlijk). Voor de uitslag moet je $R_1$ weten en die is gelijk aan $\sqrt{x^2+(65/2)^2}$ (Pythagoras) en dat is ongeveer $439.95$. In de uitslag rechts zie je de sector (taartpunt) met straal $R_1$ en booglengte $65\pi$ (de lengte van de cirkel bij diameter $65$).

Je sleeve moet in het midden aansluiten maar je schreef niet aan welke kant; ik heb beide mogelijkheden maar getekend: rood naar de punt toe, oranje van de punt af. Het midden ligt op hoogte $x+135/2=x+67.5$.
De diameter halverwege je afgeknotte kegel is gelijk aan $75$, met gelijkvormigheid volgt dat dat de straal van de rode boog in de uitslag (in het groene gebied) gelijk is aan $\eqalign{\frac{75}{65}R_1}$.
Ten slotte moet je $\ell$ nog weten; dat gaat weer met gelijkvormigheid:
$\ell:105=R_1:x$, dus $\eqalign{\ell=\frac{R_1}{105}x}$.

©2004-2024 WisFaq