Wat is de gulden snede?

Hallo, wat is de gulden snede nu precies?
Vriendelijke groet

Anoek
Leerling onderbouw vmbo-havo-vwo - maandag 12 mei 2003

Antwoord

Als ik een lijnstuk met A en B neem van 10 cm bijvoorbeeld. Dan kan ik dat natuurlijk even tekenen:

Nu kan ik ergens op dit lijnstuk een punt P kiezen waar ik maar wil...




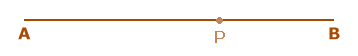
Nu is er één plek voor P waar iets heel bijzonders aan de hand is. Op die plek geldt namelijk dat PB:AP=AP:AB

We zeggen wel PB staat tot AP is hetzelfde als AP staat tot AB. Of als je het in een verhoudingstabel zet ziet het er zo uit:

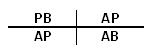
Omdat ik weet dat AB=10 en AP+PB=10 zou ik de plaats van P precies kunnen uitrekenen. Laten we dat maar eens doen!

Berekening
Laten we AP=x nemen. Er geldt dan:
AP=x
PB=10-x
AB=10

Met kruislings vermenigvuldigen in de tabel zou ik dan kunnen opschrijven:

(10-x)·10=x·x
100-10x=x²
x²+10x-100=0
(reken reken)
x$\approx$6,18033

Dus:
AP$\approx$6,18033
BP$\approx$3,81967

De gulden snede is nu de verhouding AB:AP en dat is ongeveer 1,61803. Maar de verhouding AP:PB is ook ongeveer 1,61803, want dat was de bedoeling.

Deze verhouding (lees 1,681803) heeft zelfs een apart symbool gekregen: $\Phi$ (spreek uit als Phi)

Waar is dat voor nodig?
Wat is nu het idee? Het idee is dat die P het lijnstukje verdeeld op een mooie manier. Je snijdt het lijnstuk in een bepaalde verhouding... vandaar het woord snede.

Het komt er op neer dat je dat punt P zo neer zet dat AP ongeveer 1,61803 keer zo groot is als PB. En dat is dan mooi! Zeggen ze...

De gulden snede is de verdeling van een lijnstuk in twee delen, waarvan het kleinste zich verhoudt tot het grootste als het grootste tot het geheel.

Kijk maar eens. Hopelijk kan je het een beetje volgen...

Zie The Golden section ratio: Phi

Vragen naar aanleiding van dit antwoord? Klik rechts..! maandag 12 mei 2003

©2004-2024 WisFaq