WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Kubus en bol (wiskunde olympiade)

Bij de wiskunde olympiade 2002 kwam een opgave voor:

B4: In een kubus met ribbe 6 is een bol met diameter 6. De bol raakt dus inwendig aan de zes zijvlakken van de kubus. We denken de kubus opgedeeld in 216 eenheidskubusjes van 1×1×1. Hoeveel kubusjes liggen er geheel binnen de bol? Een kubusje met een hoekpunt op het boloppervlak en verder binnen de bol tellen we mee als geheel binnen de bol liggend.

Met als uitwerking:

B4. Plaats het middelpunt van de bol in de oorsprong en beschouw een achtste deel van de kubus met een achtste deel van de bol er in. Het is duidelijk dat de kubusjes aan de buitenkant niet geheel binnen de bol liggen. Liggen alle resterende kubusjes (2x₂x₂) geheel binnen de bol? Het hoekpunt dat het verst van de oorsprong ligt, ligt op twee maal een lichaamsdiagonaallengte van de oorspong en dat is 2x√3 en dat is meer dan 3. De resterende 7 eenheidskubusjes liggen binnen de bol, want de drie hoekpunten die het verst van de oorsprong liggen, liggen op een afstand √2²+2²+1² =3 van de oorsprong en dus precies op het boloppervlak. In totaal liggen er dus 8x₇ = 56 eenheidskubusjes binnen de bol.

Ook te bekijken op http://olympiads.win.tue.nl/nwo/opgaven/index.html
Opgave B4 van 18 januari 2002

Ik begrijp er dus niets van hoe ze op die uitwerking komen zou u mij iets meer uitleg kunnen geven? want ik kom als eerste al bij de lichaamsdiagonaal uit op 3√3 terwijl zij op 2x√3 uitkomen (??) HELP! danku
marloe
Leerling bovenbouw havo-vwo - dinsdag 15 april 2003

Antwoord

Dag Marloes,

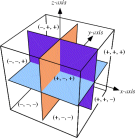
Beschouw een octant, dus een achtste deel. Zo een deel bestaat uit 3·3·3 eenheidskubusjes. Nu beweren ze (en volgens mij heb je die sprong gemist) dat de kubusjes op de 'buitenkant' van dit octant niet volledig in de bol kunnen liggen. Immers, ze hebben allemaal een punt dat coördinaten (x,y,z) heeft, waarbij één van die getallen een 3 of -3 is, en de andere twee niet allebei nul. Zo een punt kan niet volledig in de bol liggen.

Dus is het per octant alleen nodig de 2·2·2 eenheidskubusjes te bekijken die het dichtst bij de oorsprong liggen. En dan moet je voor elk kubusje kijken of het binnen de bol ligt:
- Er is één kubusje, namelijk de kubus die de oorsprong bevat, waarvoor het verste punt coörds (1,1,1) heeft. Twee keer Pythagoras levert een afstand van √3, dus binnen de bol.
- Er zijn 3 kubussen waarvan het verste punt coörds (1,1,2) of (1,2,1) of (2,1,1) heeft. Afstand: √6, dus binnen.
- Er zijn 3 kubussen waarvan het verste punt coörds (2,2,1) of (2,1,2) of (1,2,2) heeft. Afstand: 3, dus het verste punt ligt op de bol, volgens de opgave wordt ook dit goedgerekend.
- Er is één kubus waarvan het verste punt coörds (2,2,2) heeft, dus afstand tot oorsprong is √12 = 2√3 = 3,4... $>$3. Dus die ligt deels buiten de bol.

Samen dus 7 per octant, dus 56 kubusjes.

Groeten,

Christophe

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 15 april 2003