WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Inhoud tetraëder

Bestaat er een formule om de inhoud van een zo regelmatig mogelijke tetraëder te berekenen in functie van de zijde? Zo ja, hoe bewijs je die?
Vincen
3de graad ASO - maandag 14 april 2003

Antwoord

Een zo regelmatig mogelijk viervlak (zeg maar gewoon 'een regelmatig viervlak', want zo heten ze) kan je laten ontstaan door een kubus van 4 "overtollige" piramides te ontdoen (zie de figuur hieronder).

Waarom is EDBG een regelmatig viervlak?
Hoe groot is een ribbe van dat viervlak, als de ribbe van de kubus gelijk is aan a?
Zo'n overtollige piramide is bijvoorbeeld E.ABD.
Welke zijn de andere drie?
Hebben die piramides allemaal dezelfde inhoud?
De inhoud van de kubus (met ribbe a) is a³.
De inhoud van piramide E.ABD kan je berekenen met de formule ¹/₃Gh, waarbij G de oppervlakte is van driehoek ABD en h de hoogte (welk lijnstuk is die hoogte?).
Inhoud(E.ABD) = ¹/₆a³.
Dus de inhoud van het regelmatige viervlak EDBG is ¹/₃a³.
Volgens mij kan je hieruit nu zelf wel afleiden hoe groot de inhoud is van zo'n viervlak waarvan een ribbe gelijk is aan (zeg) b.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 14 april 2003

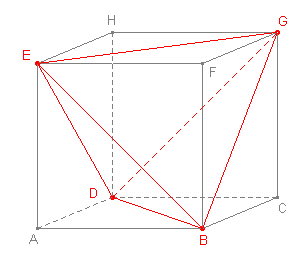
Re: Inhoud tetraëder