Dag, mijn werktempo ligt niet zo hoog, dus ben ik nog steeds met mijn zonnepaneel project bezig. Vorige probleem met arcsin is goed opgelost. Nogmaals Dank.
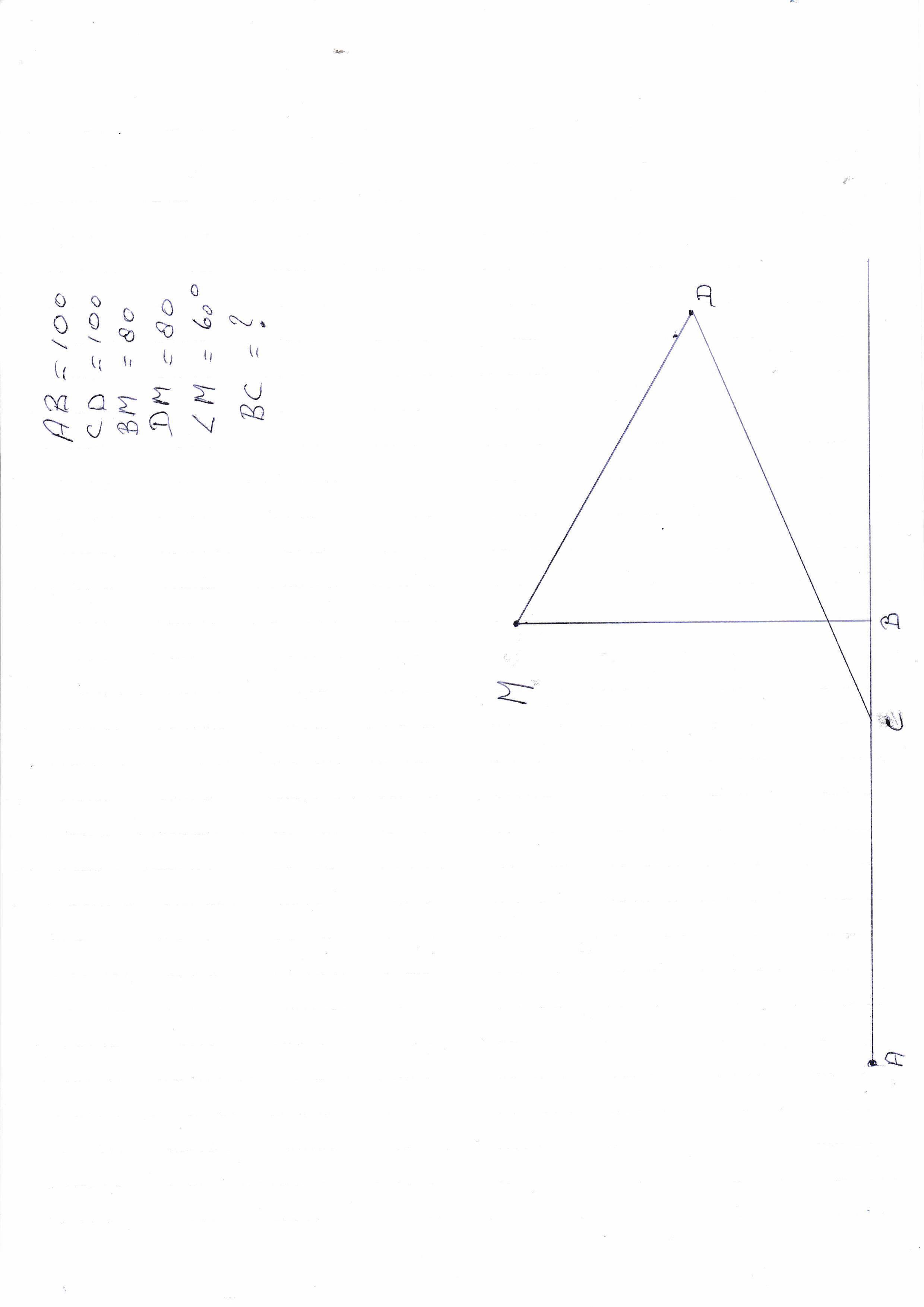
Veel probleempjes zijn opgelost, maar ik loop nu weer tegen een wiskundige vraag aan. Ik hoop dat je me nog weer een keer kunt helpen. Simpele "meetkunde" maar ik kom er niet uit. De tekening in de bijlage spreekt denk ik voor zich zelf. Misschien is de context wel van belang:
MB=MD is een zonnepaneel dat kan draaien om punt M. Begin stand is MB, MB verticaal, AB is een stang, B is bevestigingspunt aan het paneel, punt A kan bewegen over de lijn AB en duwt daardoor paneel MB richting de stand MD, waarbij de hoek M bv 60 graden wordt.
Mijn vraag is nu: hoe ver moet punt C schuiven over de lijn AB om stand MD te bereiken, dus wat is BC?
( ik vermoed dat het iets wordt van twee vergelijkingen met twee onbekenden, maar welke?)
vr gr
Teun
Teun
Student hbo - maandag 24 maart 2025
Hier is je plaatje, met wat coördinaten ingevoerd.
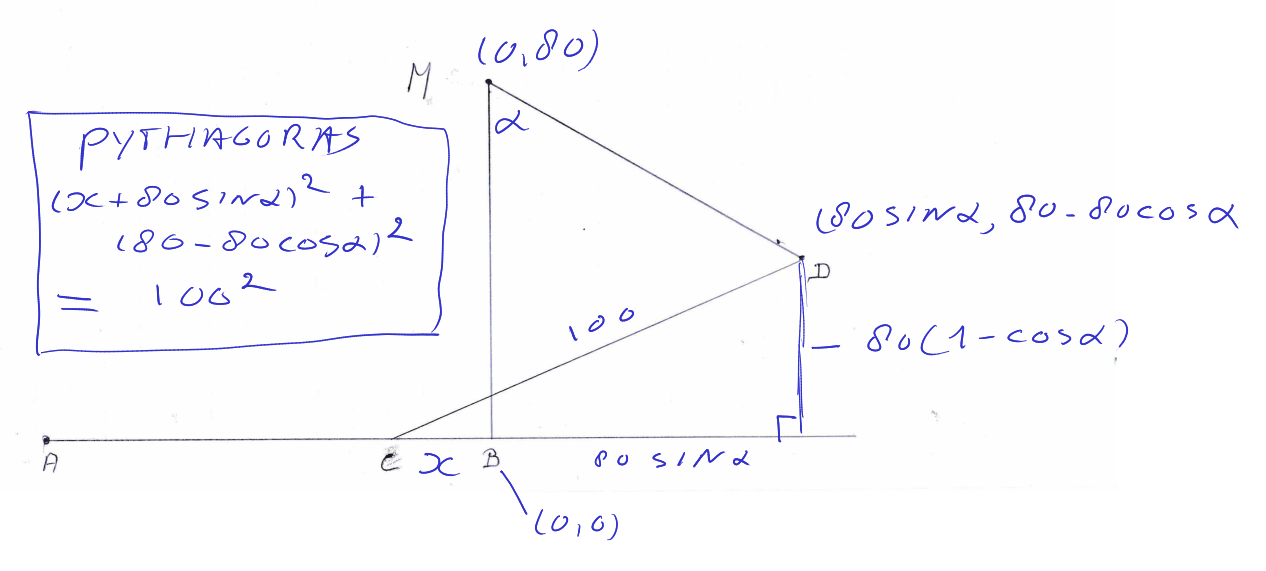
NB \alpha ligt tussen 0 en \frac\pi2 (of 0^\circ en 90^\circ), en x is positief, dus C=(-x,0).
We krijgen dus voor x=BC de volgende vergelijking:
(x+80\sin\alpha)^2=100^2-80^2(1-\cos\alpha)^2
met oplossing
x=-80\sin\alpha \pm 20\sqrt{25-16(1-\cos\alpha)^2}
Omdat x positief is moeten we dus
x=-80\sin\alpha + 20\sqrt{25-16(1-\cos\alpha)^2}
hebben.
Voor \alpha=60^\circ vul je \sin\alpha=\frac12\sqrt3 en \cos\alpha = \frac12 in:
x=-40\sqrt3 + 20\sqrt{21}









