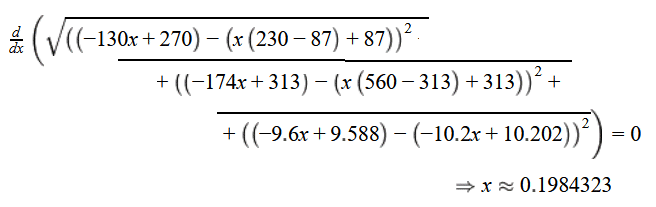|
|
|
\require{AMSmath}


Kortste afstand berekenen
Ik krijg een ander antwoord dan de uitwerking van het boek. Ik heb zelf gekeken of ik een verkeerde denkstap heb genomen, maar mij lijkt dat wat ik heb gedaan ook tot het juiste antwoord moet leiden.

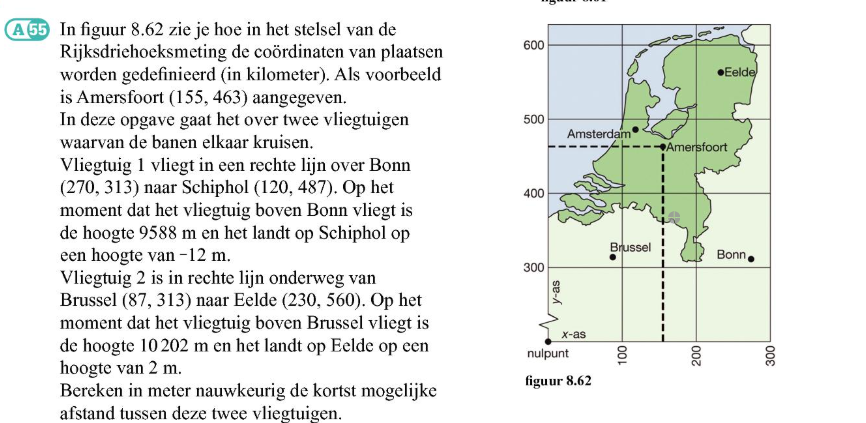
De eerste stap, de ruimtevectoren van de vliegtuigen van mij zijn gelijk aan die van de uitwerkingen. Wat anders is, is dat in de uitwerkingen een vergelijking van een vlak wordt opgesteld en daarmee de afstandsformule wordt gebruikt. Ik heb de (naar 3D uitgebreide) formule van Pythagoras gebruikt en de afgeleide daarvan gelijk gesteld aan 0. Het tijdstip waarop de afstand dan minimaal is, is dan dit berekende tijdstip. Daarna heb ik dit tijdstip weer ingevuld in de gemaakte 'Pythagoras-formule' en daarmee de afstand verkregen.
Hieronder mijn uitwerking beknopt overgetypt:
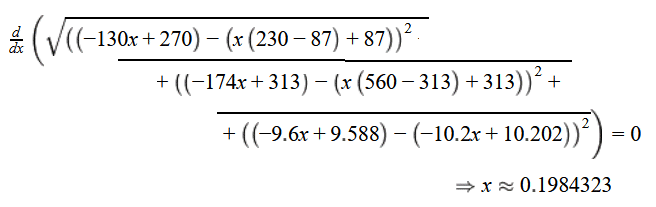
Die x weer invullen geeft ongeveer 153 544 meter als afstand en dat is veel meer dan wat er in de uitwerkingen staat. Wat klopt er niet aan mijn uitwerking?
Henk
Leerling bovenbouw havo-vwo - donderdag 20 maart 2025
Antwoord
Lees de vraag nog eens goed: er wordt gevraagd naar de kortst mogelijke afstand tussen de twee vliegtuigen. Wat er niet staat is ook belangrijk, er staat niet dat de vliegtuigen tegelijk uit Brussel/Bonn vertrekken, noch dat ze dezelfde snelheid hebben; allemaal dingen die je wel in je uitwerking hebt gestopt.
De opgave vraagt op een nogal omslachtige manier naar de afstand tussen de twee lijnen waarlangs de vliegtuigen vliegen; dichter dan die afstand kunnen ze niet bij elkaar komen, ongeacht snelheid, startijd, enzovoort. De uitwerking die je beschrijft is correct: een vlak door de ene lijn parallel aan de andere opstellen en dan de afstand van de andere lijn tot dat vlak bepalen.
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 20 maart 2025
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|