|
|
|
\require{AMSmath}


Puzzelvraag
Hallo, dit stond in mijn puzzelboek van wiskunde voor gevorderden en ik kwam er maar niet aan uit (het antwoord is 2Bgsin(1/sqrt3)), de vraag luidt:
"Een Noord-Indische piramide heeft 4 gelijkzijdige driehoeken als opstaande zijvlakken. Bepaal de hoek tussen 2 overstaande zijvlakken.”
Ik dacht dat het gewoon \pi/3 was, maar blijkbaar niet
Thomas
3de graad ASO - vrijdag 28 februari 2025
Antwoord
Hallo Thomas,
Je had vast al gevonden dat de hoogte van een gelijkzijdige driehoek met zijde 2 gelijk is aan \sqrt{} 3, zie de figuur links hieronder.
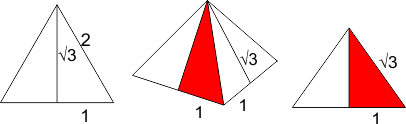
Maar bij de piramide staan de zijvlakken niet verticaal, zie de middelste figuur. De hoogte van de piramide is dus niet \sqrt{} 3. Je berekent de hoogte van de piramide door te bedenken dat in het aanzicht van de piramide (rechter figuur) de schuine zijde van de rode driehoek wordt gevormd door de hoogtelijn van de gelijkzijdige driehoek. Dan blijkt dat de halve hoek tussen 2 overstaande zijvlakken (dus: de tophoek van de rode driehoek rechts) gelijk is aan Bgsin(1/ \sqrt{} 3. De complete hoek tussen deze twee vlakken komt hiermee op 2·Bgsin(1/ \sqrt{} 3.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 28 februari 2025
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|










 Re: Puzzelvraag
Re: Puzzelvraag