WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Symmetrische functies

Hallo, ik heb echt al lang nagedacht over deze vraag maar ik snap niet hoe je er aan kan beginnen. "Een schip met een diepgang van 5 meter vaart een vissersdorp binnen. De diepte van de vaargeul van de haven is nogal onderhevig aan de werking van eb en vloed en kan in ruwe benadering beschreven worden door de functie d(t)=2,8(2+cos(t/2)) met hierbij d(t) de diepgang in meter en t de tijd in uur. De twee deelvragen zijn:

a) bereken hoelang het schip erover mag doen om de haven binnen te varen als onder de kiel nog 15% van zijn diepgang aan water nodig is om veilig te kunnen varen.

b) Welke diepgang mag een schip maximaal hebben om veilig de haven te kunnen binnenvaren als de reis van de ingang van de haven tot de aanlegsteiger een duur duurt?

Hetgeen ik al opgemerkt heb bij vraag b is dat het een even functie is want cosx = cos-x maar verder dan dat kom ik niet. Ik vind het ook een beetje moeilijk om de grafiek te interpreteren, ik snap niet zo goed wat het voorstelt en zo.

Groetjes Eleonore
Eleonore
Leerling bovenbouw havo-vwo - donderdag 27 februari 2025

Antwoord

Hallo Eleonore,

Om de vragen a) en b) te kunnen beantwoorden, moet je de grafiek goed kunnen interpreteren. Ik begin dus met jouw laatste vraag: wat stelt de grafiek eigenlijk voor?

In de figuur hieronder zie je de grafiek van d(t). De horizontale as loopt van x=0 tot x=24, deze geeft dus de tijd weer gedurende 24 uur vanaf t=0. Verticaal staat de diepte d van de vaargeul. Ik heb ik gekozen: Y_min=0 en Y_max=10.

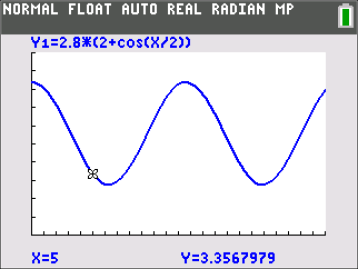
In de grafiek kan je voor elk tijdstip aflezen wat de diepte van de vaargeul op dat moment is. Als voorbeeld zie je dat voor X=5 (dus: 5 uur na t=0) de diepte afgerond 3,36 meter is.

Nu de vragen:
De diepgang van het schip is 5 meter. Om veilig te varen moet onder de kiel nog 15% extra waterhoogte zijn, dus het schip kan veilig varen als de diepte van de vaargeul minimaal 1,15·5=5,75 meter is. In de figuur hieronder heb ik de grafiek van Y=5,75 toegevoegd:

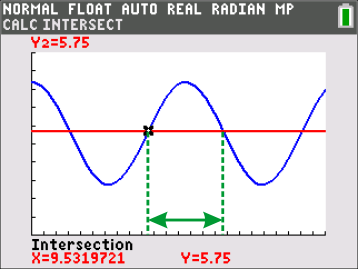
In de figuur zie je dat in de periode tussen de twee aangegeven snijpunten (zie de groene pijl) de diepte d groter is dan de vereiste 5,75 meter. In deze periode kan het schip dus veilig naar de haven varen. Het eerste snijpunt heb ik voor je berekend: ik vind (afgerond) X=9,53, dus de veilige periode start 9,53 uur na t=0. Bereken zelf het snijpunt aan het einde van de veilige periode. het verschil in tijd geeft je het antwoord op vraag a).

Voor vraag b) moet je zien te berekenen hoe hoog de rode grafiek mag liggen, zodanig dat de tijd tussen de snijpunten één uur is. Bedenk hiervoor dat de grafiek rond een top symmetrisch is: de tijd tussen een top en het rechter snijpunt is dus een half uur. Nu komt het goed uit dat de grafiek bij t=0 precies een top heeft (begrijp je waarom?). Bereken dus de waterdiepte d voor t=0,5. Dit is 115% van de maximale diepgang van een schip. Reken terug naar 100% om de maximale diepgang van het schip te berekenen.

Lukt het hiermee?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 28 februari 2025

Re: Symmetrische functies