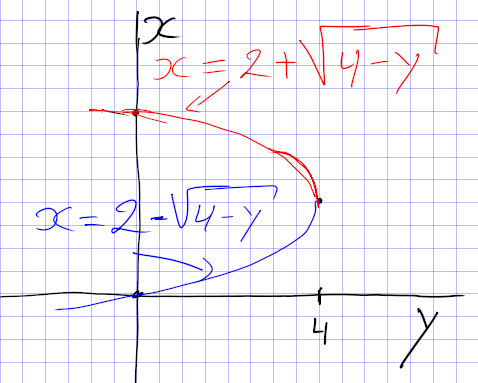WisFaq!

Loading jsMath...

De digitale vraagbaak voor het wiskundeonderwijs

HOME

\require{AMSmath}

Wentelen om y-as

Geachte,
Graag uw hulp bij het volgende probleem:
Wat is de inhoud van het omwentelingslichaam bij wentelen om de y-as van y = 4x-x² tussen de grenzen x=0 en x=4?
Ik heb een tekening gemaakt van een vierkant van 4x4 vanuit O grenzend aan de positieve x en y-as met daarin de parabool. Het vierkant verdeeld in 3 delen: een linker gebied, het gebied onder de parabool en het rechter gebied. Het gaat (denk ik) om de omwenteling van het gebied onder de parabool. Het antwoord is 128/3 \pi .
Ik probeer eerst de inhoud te berekenen van het gewentelde linkergebied.
x²= 8 - y + wortel(4-y).
Inhoud = \pi integraal [( \sqrt{} (4-y)+2))². Met als grenzen 0 en 4. Hopelijk is de omzetting van de formule goed... (x en y omgewissweld). Hier komt 45 en 1/3 \pi uit. Dit lijkt me niet mogelijk, omdat de inhoud van het hele gewentelde vierkant 64 \pi is???
Ik begrijp niet waar ik de mist in ga...

Bij voorbaat dank.

Diana
Leerling bovenbouw vmbo - donderdag 13 februari 2025

Antwoord

Ik zie twee momenten: Ik zie niet waar x^2=8-y+\sqrt{4-y} vandaan komt. Maar in de volgende regel heb je alsnog 2+\sqrt{4-y}, en die moet je wel hebben. Maar je mist de tweede helft van de parabool.

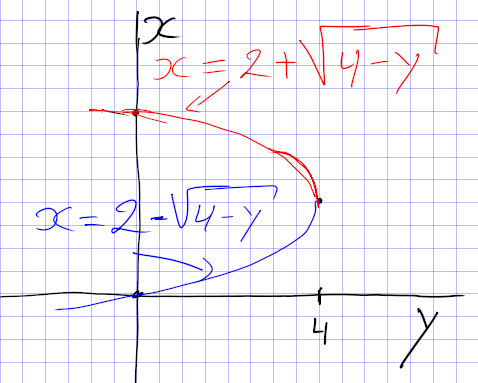
Ik heb in het plaatje even x als functie van y getekend, en jouw integraal geeft de inhoud van het wentellichaam van het rode deel van de parabool. Maar daar moet je de inhoud van het wentellichaam van het blauwe deel nog van aftrekken.
Het gaat dus om
\pi\int_0^4(2+\sqrt{4-y})^2\,\mathrm{d}y - \pi\int_0^4(2-\sqrt{4-y})^2\,\mathrm{d}y
Als je dat uitwerkt hou je
\pi\int_0^48\sqrt{4-y}\,\mathrm{d}y
over, en die heeft inderdaad de waarde \frac{128}3\pi.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 13 februari 2025