|
|
|
\require{AMSmath}



Re: Winkans multi-winlijn fruitautomaat
Ik bedoelde inderdaad diagonaal ipv verticaal. excuses.
Verder lijkt het me helemaal niet zo onduidelijk.
Er zijn inderdaad 4 verschillende symbolen, die dus op elk van de 9 posities kunnen vallen.
3 rollen met elk 3 symbolen dat lijkt me toch duidelijk.
Eenvoudiger mischien: op elk van de 9 posities valt 1 van de 4 symbolen.
Maar de kans welk symbool valt per positie is er een op een schaal van 100.
Dus stel dat ik als symbolen een kers, citroen, meloen en ster heb en ik wil voor rol 1, symbool 1 (of positie 1) weten wat de kans dat hij daar valt is dan zou dat bijvoorbeeld kunnen zijn:
kers 40 op 100
citroen 30 op 100
meloen 20 op 100
ster 10 op 100
3 kersen op een lijn levert 10 punten op.
3 citroenen 20
3 meloenen 200
3 sterren 1000
Dus concreet is mijn vraag hoe bereken ik wat per keer gokken de kans is dat je iets wint. en liever nog wat er dan aan punten word uitgekeerd. Dat zou rond de 90% moeten zijn.
Mischien maakt het nog uit dat je elke keer met 5 punten gokt.
Ik hoop dat u er deze keer wel iets mee kunt.
Bedankt voor de moeite.
Is het zo nog duidelijker?
Jeroen
Iets anders - zondag 13 april 2003
Antwoord
Leuk zo'n spraakverwarring! Je fruitautomaat bestaat uit drie rollen met 4 verschillende symbolen (in een bepaalde verhouding). In het venster zijn drie rijen symbolen te zien met 5 winrijen: 3 horizontaal en 2 diagonaal.

Per rol geldt:
P(k)=0,4
P(c)=0,3
P(m)=0,2
P(s)=0,1
En vervolgens gelden de volgende prijzen:
kkk: 10
ccc: 20
mmm: 200
sss: 1000
Tot zover lijkt het duidelijk. Voor één winlijn (zeg de middelste horizontale lijn) heb ik na 4000 keer spelen de volgende verdeling:
kkk: 241
ccc: 100
mmm: 44
sss: 8
Totaal uitgekeerd bedrag €21210,-
(VU-stat simulatie fruitautomaat)
Dus met een inleg van 5 munten (€20.000,-) lijdt de exploitant van dit apparaat (in dit geval) al een verlies van €1210,-. En dan hebben we dus alleen over één winlijn! Er waren er echter 5, dus dat wordt niks!
Laten we eens gaan rekenen! We gaan de kans uitrekenen op P(kkk), P(ccc),... voor één winlijn en verwachtingswaarde van de uit te keren prijs.
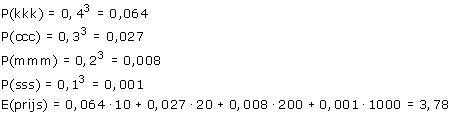
Dus dat valt nog mee... kennelijk hadden we 'geluk' bij de simulatie. Het zit hem natuurlijk in de 8 keer drie sterren. Op basis van de berekening mogen we, bij 4000 keer spelen, ongeveer 4 keer drie sterren verwachten.
Let op: we hebben de vraag alleen beantwoord voor één winlijn. Eigenlijk maakt het niet eens uit welke... maar blijft de vraag: hoe zit het nu met 5 winlijnen?
...tja en dan haak ik af. Je kunt niet zeggen dat wat geldt voor één winlijn ook geldt voor de andere vier lijntjes. Je weet immers niet of de gebeurtenis dat daar ook een prijs valt onafhankelijk is van dat eerste lijntje. Hierbij speelt de volgorde van de symbolen op de rollen ook nog een rol... Anders gezegd: dat wordt ingewikkeld.... Anders gezegd: dat wordt ingewikkeld....
Eens kijk of we dat kunnen laten zien. Hier zie je twee voorbeelden van verschillende indelingen van de rollen. De vraag is: is de kans op winnen op een andere lijn als je iets wint op één lijn bij het eerste en het tweede voorbeeld anders?

Maar misschien heb je hier wel even genoeg aan, dan denk ik vast eens na over de rest...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 14 april 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 9775
Dit is een reactie op vraag 9775 
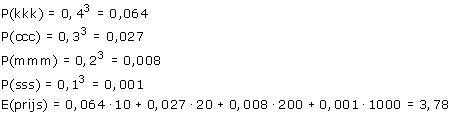
 Anders gezegd: dat wordt ingewikkeld....
Anders gezegd: dat wordt ingewikkeld.... 

