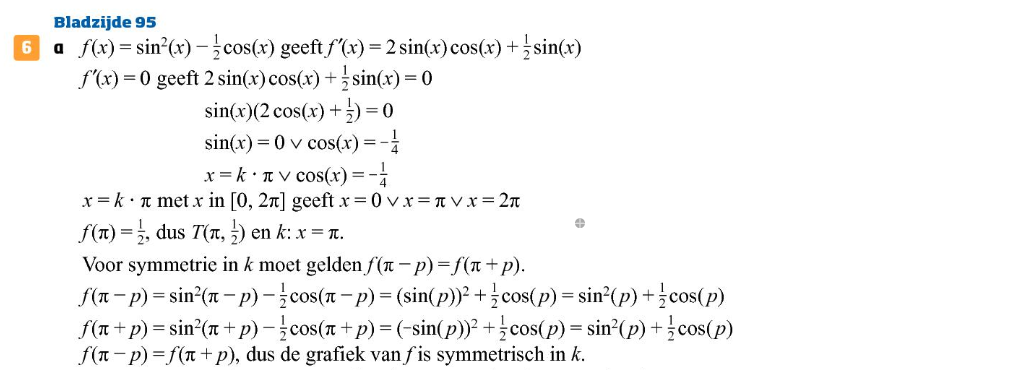WisFaq!

Loading jsMath...

De digitale vraagbaak voor het wiskundeonderwijs

HOME

\require{AMSmath}

Re: Cosinus niet in eenheidscirkel

Dit is een reactie op vraag 98362

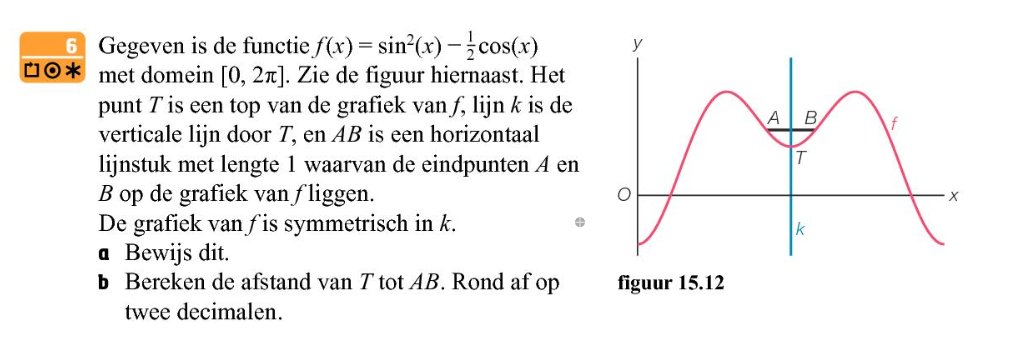
Opgave in bijlage.
Mark
Leerling bovenbouw havo-vwo - dinsdag 29 oktober 2024

Antwoord

Ik heb de uitwerking hier ingeplakt:

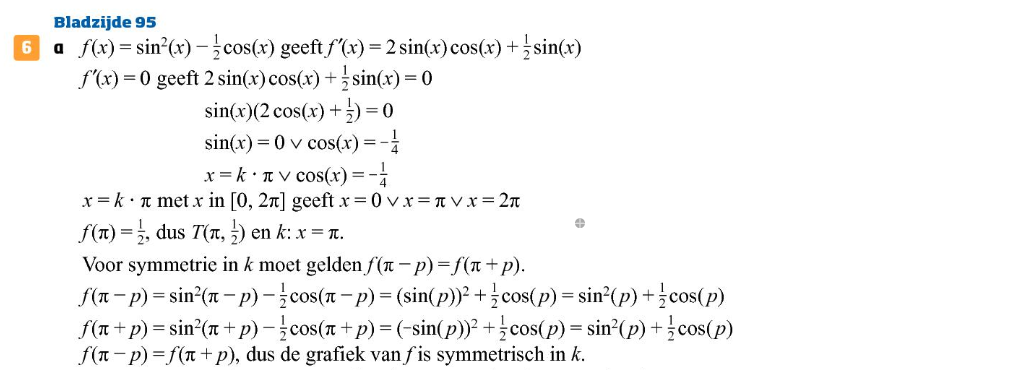
Die uitwerking verdient niet de schoonheidsprijs (de som ook niet vind ik). Er zou op zijn minst uitgelegd moeten worden waarom het geval \cos(x)=-\frac14 terzijde wordt gelegd. En ook vertelt men niet waarom \pi de juiste waarde is, en ook niet waarom er bij \pi een top ligt.

Je zou ook als volgt kunnen redeneren: als de functie symmetrisch ten opzichte van k is moet k wel door (\pi,0) (het midden van het interval [0,2\pi]) gaan.
(Ik denk dat dat ook de gedachte achter de uitwerking in het boek is: kijken of \pi bij de x-en zit met f'(x)=0; maar dat kun je ook doen door gewoon invullen.)
Dus ik bewijs dat f symmetrisch is ten opzichte van \pi en dat f voor x=\pi een top heeft.

Het eerste is makkelijk als je bedenkt dat \cos(\pi+x)=\cos(-(\pi+x))=\cos(-(\pi+x)+2\pi)=\cos(\pi-x), en ook dat \sin^2(x)=1-\cos^2(x). Dan komt er
f(\pi+x)=1-\cos^2(\pi+x)-\frac12\cos(\pi+x)=1-\cos^2(\pi-x)-\frac12\cos(\pi-x)=f(\pi-x)

Het tweede ook: f'(x)=2\sin(x)\cdot\cos(x)+\frac12\sin(x)=\sin(2x)+\frac12\sin(x), dus f'(\pi)=0; verder geldt f''(x)=2\cos(2x)+\frac12\cos(x), dus f''(\pi)=\frac32 en dat is positief, dus bij \pi zit een lokaal minimum.

Overigens kun je voor de punten waar \cos(x)=-\frac14 geldt op deze manier laten zien dat daar een lokaal maximum zit want je kunt f''(x) schrijven als 4\cos^2(x)-2+\frac12\cos(x), dan heb je x niet nodig want je kunt meteen -\frac14 voor elke \cos(x) invullen. Het resultaat is -\frac{15}8 en dat is negatief.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 29 oktober 2024