|
|
|
\require{AMSmath}



Langste kortste weg tussen twee punten
Hallo,
Ik heb een vraag. Hoe bereken je de langste weg op een balk? Ik kon helaas geen bronnen vinden over hoe je de langste weg moet vinden, maar wel over hoe je de kortste weg moet vinden.
Ik bedoel ook niet letterlijk de langste weg tussen twee punten, aangezien het oneindig kan zijn, maar eigenlijk eerder de langste kortste weg als je het begrijpt. Het moet de langst mogelijke weg zijn tussen twee punten, maar het moet ook een rechte lijn zijn.
Alvast bedankt,
Mvg,
Milad 
Milad
Leerling bovenbouw havo-vwo - woensdag 29 mei 2024
Antwoord
Hallo Milad,
Wellicht heb je de vraag kortste weg tussen twee punten in gedachten. Hierbij is het de bedoeling om de kortste weg tussen de punten B en H te vinden over de zijden van een balk:

Zoals je in het antwoord kunt lezen, is het een kwestie van uitslagen tekenen om de kortste, dus rechte lijn te vinden tussen de twee punten.
Je merkt terecht op dat er geen langste weg bestaat, want onderweg kan je oneindig lang in rondjes draaien. Maar er is ook geen langste rechte weg, zoals je in onderstaande figuur kunt zien:

Je kunt in een rechte lijn meerdere keren rond de balk lopen. Als je de wikkelingen maar dicht genoeg bij elkaar legt, wordt de route ook onbegrensd lang.
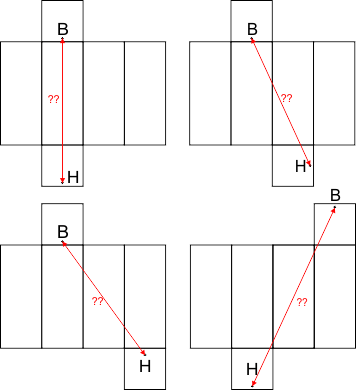
Wellicht bedoel je dat je maar één keer over elk vlak mag lopen. In dat geval is het, net als bij het vinden van de kortste route, een kwestie van uitproberen. Teken meerdere uitslagen, trek een rechte lijn tussen de punten B en H en bereken met Pythagoras de lengte van deze lijn. Hieronder heb ik enkele mogelijke uitslagen getekend:

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 29 mei 2024
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|














 Re: Langste kortste weg tussen twee punten
Re: Langste kortste weg tussen twee punten