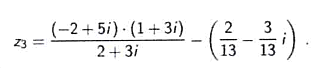De digitale vraagbaak voor het wiskundeonderwijs

home |  vandaag |  gisteren |  bijzonder |  gastenboek |  wie is wie? |  verhalen |  contact

HOME

samengevat

vragen bekijken

een vraag stellen

hulpjes

zoeken

FAQ

links

twitter

boeken

help

inloggen

colofon

Re: Reëel en imaginair deel van complexe getallen berekenen

Dit is een reactie op vraag 98168

Nogmaals bedankt voor de moeite!

Y
3de graad ASO - dinsdag 23 april 2024

Antwoord

Complex delen doe je door teller en noemer met de complex toegevoegde van de noemer te vermenigvuldigen. De breuk in je som wordt dan

\frac{(-2+5i)\cdot(1+3i)\cdot(2-3i)}{(2+3i)\cdot(2-3i)}= \frac{(-2+5i)\cdot(1+3i)\cdot(2-3i)}{13}

Nu de teller netjes uitvermenigvuldigen en dan nog de andere term aftrekken.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..! dinsdag 23 april 2024

home |  vandaag |  bijzonder |  gastenboek |  statistieken |  wie is wie? |  verhalen |  colofon

©2001-2025 WisFaq - versie 3