WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Limiet recursieve functie

f(n) is gedefinieerd als volgt: voor n=0 geld f(n) = 1, anders is f(n) gelijk aan f(n-1)+¹/_f(n-1), nu is mijn vraag: 'Convergeert deze functie? Zo ja, wat is lim_{n $\to $ $\infty $}(f(n)) dan?'

Heel erg bedankt voor uw hulp!
Oliver Ruiz Lopez
1ste graad ASO-TSO-BSO - zondag 24 maart 2024

Antwoord

Merk allereerst op dat de rij stijgend is:
$$f(n)=f(n-1)+\frac1{f(n-1)} > f(n-1)
$$Teken de webgrafiek van de getallenrij die je zo krijgt:

Dat suggereert dat de waarden onbeperkt toenemen, en dat de rij divergeert.

Inderdaad: als de rij zou convergeren naar $L$ dan zou $L$ aan de vergelijking $L=L+\frac1L$ moeten voldoen, maar die heeft geen oplossing, dus $\dots$

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 24 maart 2024

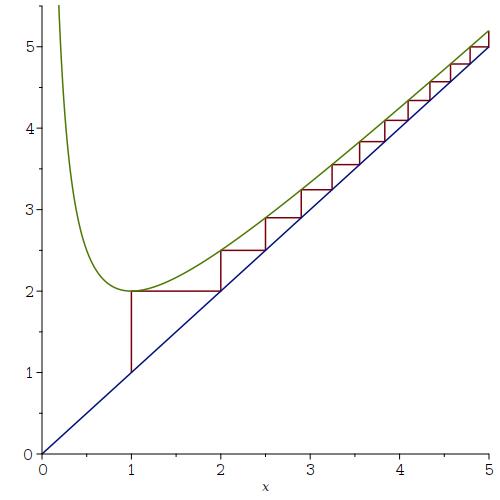
Re: Limiet recursieve functie