WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Construeer driehoek ABC

Construeer driehoek ABC wanneer gegeven zijn : de lengtes van hoogtelijn, zwaartelijn en bissectrice vanuit C
Niet willekeurige lengtes zijn mogelijk.
Begin met een willekeurige driehoek ABC en teken daarin de hoogtelijn zwaartelijn en bissectrice vanuit tophoek C. Verwijder AC en BC en tracht daarna de driehoek te construeren.
Ik heb lang geleden de oplossing gehad, maar die kan ik niet meer vinden.
Ik ben nu 85, eindexamen gym B Nederlansch Lyceum Den Haag 1956
Jan Nu
Iets anders - dinsdag 15 augustus 2023

Antwoord

Hey Jan,

Die driehoek is niet eenduidig en het probleem is niet altijd oplosbaar. Ik zal dat tussendoor proberen duidelijk te maken. Ik ga maar eens uit van een driehoek met 3 scherpe hoeken. Je hebt hierbij van een dergelijke driehoek de eigenschap nodig dat de middelloodlijn van AB en de bissectrice uit C elkaar snijden op de omgeschreven cirkel van driehoek ABC. In het volgende plaatje zie je dat gebeuren.

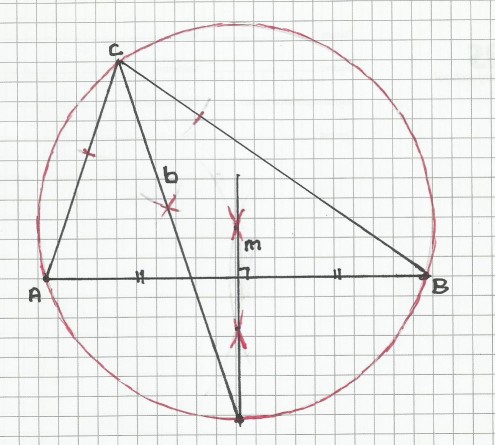
Je kunt ook zien dat het niet gaat lukken wanneer de driehoek vanuit tophoek C gelijkbenig is, Dan zijn namelijk ook de hoogtelijn, zwaartelijn, bissectrice en de middelloodlijn van AB identiek.

Nu de constructie. Ik heb hier staan lengtes h=5, b=5.3 en z=5.9

Stap(1): Begin met het tekenen van de hoogtelijn vanuit C in een willekeurige richting. Bij een andere richting draait de driehoek maar de vorm blijft gelijk. Teken nu de lijn loodrecht op het uiteinde van de hoogtelijn. Op deze lijn l(A,B) liggen straks ook de hoekpunten A en B.

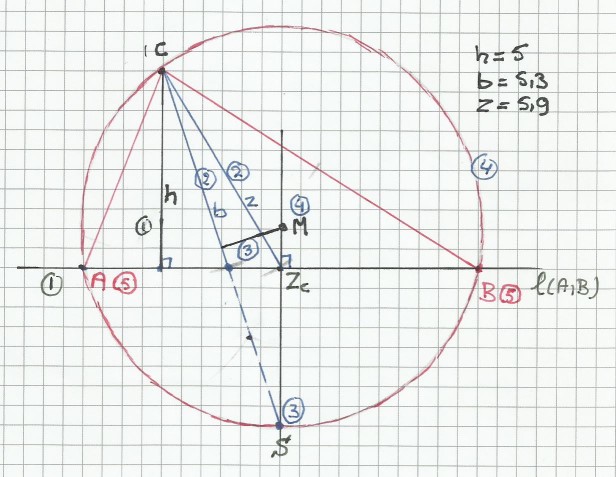
Stap (2): Teken nu m.b.v. de gegeven lengtes de bissectrice vanuit C en de zwaartelijn vanuit C. Noem het snijpunt Z_c. Dit punt is nu het midden van AB (nb als je de zwaartelijn aan de andere kant van de hoogtelijn plaatst krijg je een gespiegelde driehoek)
Stap (3): Teken nu de middelloodlijn van AB en snijd deze met de verlengde bissectrice, snijpunt S
Stap (4): Gebruik nu de eigenschap dat S op de omgeschreven cirkel van driehoek ABC ligt, net als punt C. Het middelpunt van deze cirkel is het snijpunt M van de middelloodlijn van AB en de middelloodlijn van CS. Nu kan je de omgeschreven cirkel tekenen en de snijpunten hiervan met l(A,B) levert de andere twee hoekpunten van de gezochte driehoek.

Met vriendelijke groet
JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 17 augustus 2023