|
|
|
\require{AMSmath}



Opbrengstmodellen
Dit is een vraag uit het examen van wiskunde 2002:
In de economie wordt vaak gebruik gemaakt van wiskundige modellen. Daarin komen formules voor die een theoretisch verband beschrijven tussen economische grootheden. Een producent verkoopt q eenheden van een product. De totale opbrengst is TO. Als we willen weten hoe de totale opbrengst verandert bij een kleine toename van q, dan kijken we naar de marginale opbrengst MO.
Stel dat voor het verband tussen q en TO een formule van de volgende vorm geldt: TO = -0,01∑q3+ b∑q2 met b een positief getal. Bij elke waarde van b kan het maximum van TO worden berekend. De waarde van q waarbij dit maximum optreedt, hangt af van b. Deze waarde van q noemen we qmax. De vraag is nu om een grafiek te tekenen van het verband tussen qmax en b.
Volgens mij moet je daarvoor de afgeleide van TO bepalen, maar omdat je daar allerlei getallen voor kan invullen snap ik niet hoe je dit moet doen. Klopt wat ik denk? Hoe moet ik verder?
S
Leerling bovenbouw havo-vwo - zaterdag 12 april 2003
Antwoord
Beste Sabine,
Je zit in de buurt, maar je bent er nog niet helemaal. Dat je de oplossing niet kent, moet je niet erg vinden, want dat ligt niet voor de hand (wegens de economische achtergrond van de vraag). Hoewel je met al de gegevens uit de opgave (en een goede kennis van de wiskunde) er wel zelf op kunt komen.
Ik ga iets te veel extra informatie geven zodat je goed begrijpt waar de oplossing vandaan komt. Niet alle stappen zijn nodig in het antwoord. Je idee is al goed: het heeft heel wat te maken met de marginale opbrengsten. En uit de omschrijving in de opgave (wijziging van de totale opbrengsten bij een superkleine wijziging van de hoeveelheid q) heb je al wel door dat de marginale opbrengsten (MO) gewoon de afgeleide is van de totale opbrengsten (TO). Het moeilijkse zit er in dat er een "speciaal" verband is tussen MO en TO die niet expliciet in de opgave staat, maar die je wel kunt afleiden.
Laten we de TO-functie eens van dichterbij bekijken. Ik heb ze hieronder uitgetekend (voor de eenvoudigheid heb ik b constant genomen en b = 1).
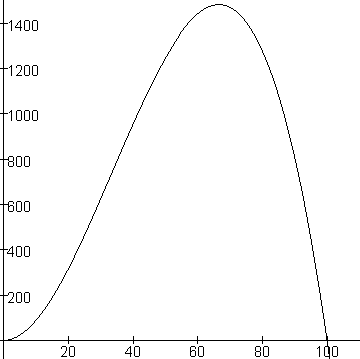
Opgelet: er zit een "verhaaltje" achter: de hoeveelheid kan dus nooit negatief zijn (minder dan niets verkopen gaat niet, dus q  0 negeren we). 0 negeren we).
De functie is niet handig, waardoor het volgende niet echt duidelijk te zien is, maar geloof me maar dat dat klopt. Ik heb de bovenstaande figuur verdeeld in 3 cruciale delen.
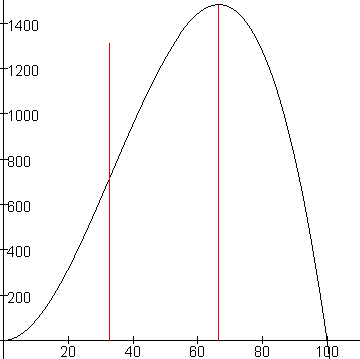
In het eerste deel stijgt de functie sterker dan evenredig, in het tweede deel minder dan evenredig (er is een vrij lange overgangszone waardoor je het niet goed ziet). Op de overgang tussen het tweede en het derde deel is het maximum (q is ongeveer 65). Vanaf het derde deel dalen de opbrengsten en vanaf q = 100, maakt het bedrijf verlies. De optimale productiegrootte is dus waar TO = maximaal.
Voor elk deel reageren de marginale opbrengsten ook. Deze zijn dus de afgeleide van de functie, of anders uitgedrukt de raaklijn aan de functie. Beeld je in dat je in elk punt een denkbeeldige raaklijn trekt en deze vergelijkt met de raaklijn in het volgende punt. In het eerste deel heeft de raaklijn een positieve helling (MO is positief) en als je kijkt met de vorige raaklijnen moet je vaststellen dat de helling steeds groter wordt (groter wordende richtingscoŽfficient ofwel MO stijgt). In het tweede deel wordt de helling kleiner (MO daalt) en de richtingscoŽfficiŽnt daalt totdat ze 0 wordt in het maximum van de TO-curve. In dit punt geldt: MO = 0. In het derde deel is er een negatieve helling van de raaklijn en is MO ook dalend.
Hetzelfde kan je ook logischer wijze beredeneren (maar dat leidt ons wat te ver) of ook gewoon rechtstreeks via de afgeleide. MO = afgeleide van TO = -0,03*q2+2bq (met b = 1 genomen). Dan kan je deze functie ook grafisch tekenen en vergelijken met de TO-curve. (= beste methode voor tijdens een examen).
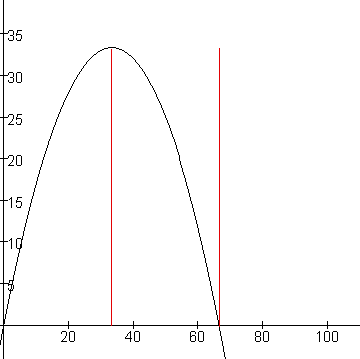
Je merkt hier duidelijk hoe TO en MO van elkaar afhangen. In dezelfde punten bereiken ze een andere fase. Wat voor jouw vraag enkel van belang is, is om te kijken naar het punt waar TO maximaal is. Je ziet dat MO dan gelijk is aan 0. Dan kan je eenvoudig verder.
qmax = MO = 0 MO = 0
qmax = -0,03*q2+2bq = 0 -0,03*q2+2bq = 0
= -0,03*qmax2+2b*qmax = 0 -0,03*qmax2+2b*qmax = 0
herschrijven als b = ... en uittekenen als grafiek
Je hebt de verschillende waarden van b dus eigenlijk niet nodig.
Groetjes,
Tom

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 12 april 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|









 0 negeren we).
0 negeren we). 

 MO = 0
MO = 0 
