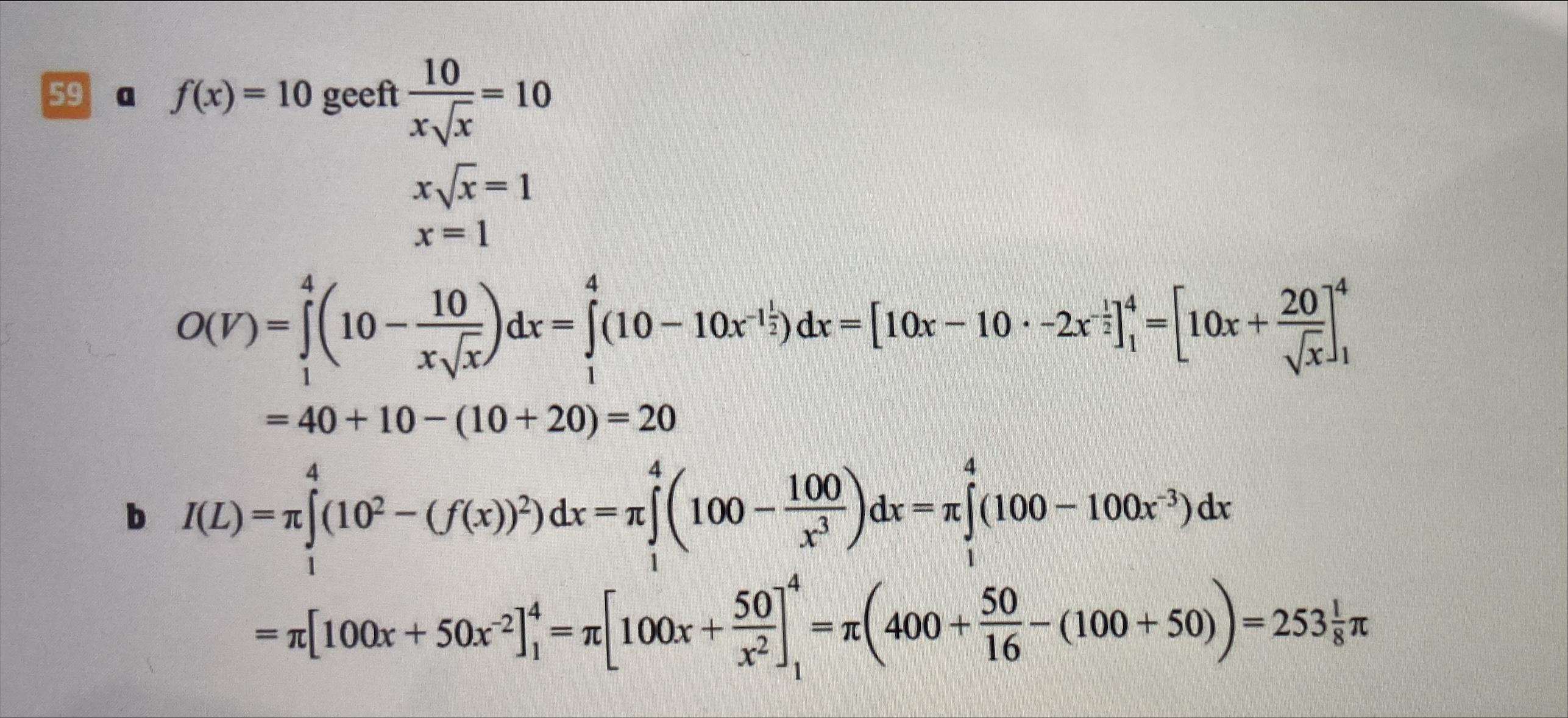WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Inhouden met vlakdelen om de x-as of cilinder

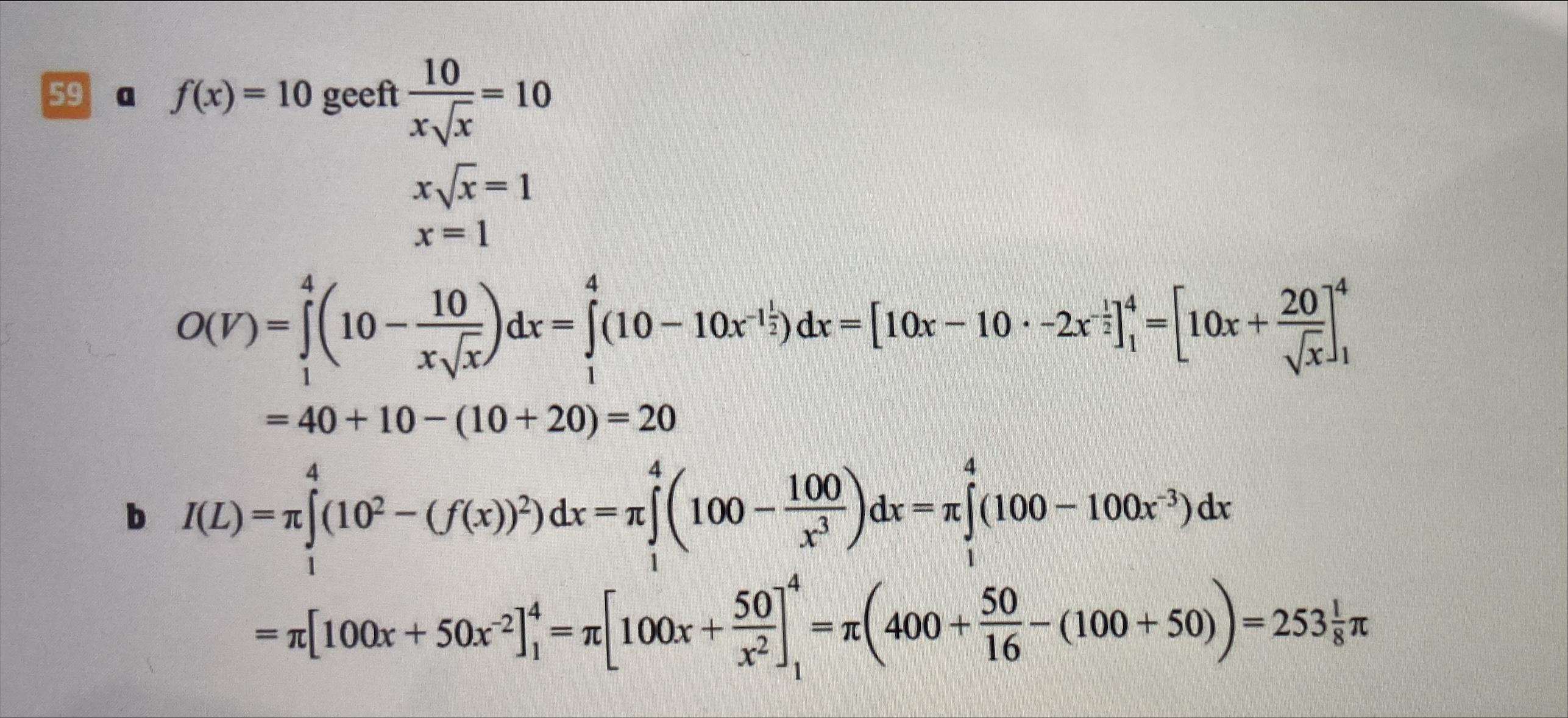
Waarom werken ze bij 62b niet met vlakdelen wentelen om de x-as maar met een cilinder ik zie geen verschil met opgave 59 waarbij dit wel werkt?
Tim
Leerling bovenbouw havo-vwo - zondag 3 juli 2022

Antwoord

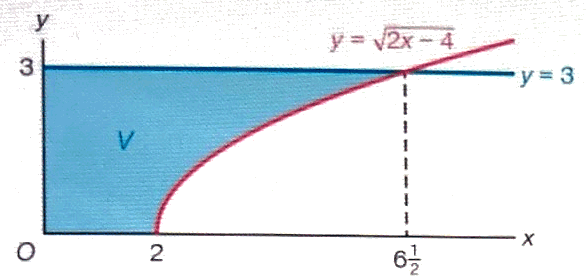
Als je 't op dezelfde manier zou aanpakken als bij opgave 59 dan krijg je de inhoud van een cilinder met hoogte 2 en straal 3 en de inhoud van het omwentelingslichaam bij het vlakdeel boven de grafiek. Dat is misschien niet 'echt' handig, maar niet onmogelijk.

$
\eqalign{
& I = I_{cilinder} + I_{omwentelingslichaam} \cr
& I = \pi \cdot 2 \cdot 3^2 + \pi \cdot \int\limits_2^{6.5} {\left( {3^2 - \left( {f(x)} \right)^2 } \right)} \cr
& I = 18\pi + \pi \cdot \int\limits_2^{6.5} {\left( {9 - \left( {\sqrt {2x - 4} } \right)^2 } \right)} \cr
& I = 18\pi + \pi \cdot \int\limits_2^{6.5} {\left( {9 - 2x + 4} \right)} \cr
& I = 18\pi + \pi \cdot \int\limits_2^{6.5} {\left( {13 - 2x} \right)} \cr
& I = 18\pi + \pi \cdot \left[ {13x - x^2 } \right]_2^{6\frac{1}
{2}} \cr
& I = 18\pi + \pi \cdot \frac{{81}}
{4} \cr
& I = 38\frac{1}
{4}\pi \cr}
$

't Is handiger om de inhoud van het omwentelingslichaam onder de grafiek te bepalen en dat dan af te trekken van de inhoud van de cilinder met hoogte $6\frac{1}{2}$.

Kortom: meestal is het slim om het handig aan te pakken...

Naschrift
Nu ik er nog 's over nadenk gebruiken ze bij de uitwerking ook een cilinder en dat geldt ook voor mijn uitwerking. Die $3^2$ is niets anders dan het kwadraat van de straal van de cilinder van 2 tot 6$\frac{1}{2}$ met een straal van 3. Eigenlijk is dat niet zo heel duidelijk als uitwerking, maar kennelijk wel gebruikelijk in bepaalde kringen...

Maar misschien was het handiger geweest om het meteen goed uit te leggen met die cilinders zodat opgave 62 dan niet ineens iets anders leek terwijl het eigenlijk allemaal één pot nat is.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 3 juli 2022