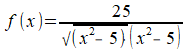WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Irrationale functie en rationale functie tekentabel

Hallo,
Ik zou een tekentabel moeten opstellen van de functie:

25/(($\sqrt{}$ x²-5)(x²-5)).

Ik weet dat de rij van de teller geheel positief zal zijn. Nu met de rij van de noemer zit ik vast. Ik denk dat de nulwaarden x=$\sqrt{}$5 en -$\sqrt{}$5. Nu vraag ik mij enerzijds af of dit dubbele nulwaarden zijn en anderzijds hoe de rij van de noemer in de tekentabel er uit ziet.

Hoe weet ik bijvoorbeeld dat het teken helemaal rechts of links van mijn rij positief of negatief zal zijn? Dit is een hele boterham alvast bedankt!
Gert
3de graad ASO - woensdag 18 mei 2022

Antwoord

Hallo Gert,

Ik neem aan dat je bedoelt:

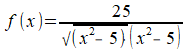
Het deel onder de wortel mag niet negatief zijn, dus geldt in ieder geval:

x²-5$ \ge $ 0.

Maar omdat je niet door nul kan delen, geldt:

x²-5 $>$ 0.

De functie bestaat dus alleen voor x $<$ -√5 of x $>$ √5

Binnen deze intervallen is de noemer positief, dus ook de gehele functie is positief. Dit levert als tekenschema:

x $<$ -√5: f(x) is positief
-√5$ \le $ x$ \le $ √5: f(x) bestaat niet
x $>$ √5: f(x) is positief

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 19 mei 2022