WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

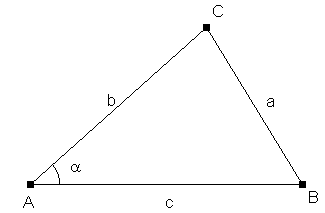
Oppervlakte driehoek

Als ik met goed herinner bestaat er een formule om met behulp van gonio de opp. van de driehoek te berekenen als je beschikt over de lengtes van de drie zijden maar niet over de hoogte. Hoe was die formule ook al weer?
Evelyn
Ouder - woensdag 9 april 2003

Antwoord

Er zijn verschillende manieren om dit aan te pakken, maar omdat je zelf al zegt dat het met gonio kan, denk ik dat het om de volgende formule gaat.
Gegeven driehoek ABC, met zijden a, b en c, en hoeken a, b en g.

De oppervlakte van de driehoek is dan gelijk aan ¹/₂·b·c·sin(a)
De hoek a kun je weer berekenen met de cosinusregel:
a²=b²+c²-2·b·c·cos(a).
Misschien heb je ook iets aan de zogeheten s-formule: s is de halve omtrek van de driehoek.
s=¹/₂(a+b+c)
Voor de oppervlakte O van driehoek ABC geldt dan:
O=Ö(s·(s-a)·(s-b)·(s-c))
groet, Anneke

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 9 april 2003