|
|
|
\require{AMSmath}



Hoe kan je het beste een breuk vereenvoudigen?
Hoe kan je stapsgewijs het beste een breuk vereenvoudigen? Zijn er speciale truukjes die je kan toepassen met je rekenmachine en/of door welk getal begin je de noemer en teller te delen?
Ik geef een paar voorbeelden en zou graag willen horen hoe deze het beste te vereenvoudigen.
26/36 , 34/51, 15/-21, -18/74 en 1008/1080
Bij voorbaat dank!
Serdal
Student hbo - dinsdag 1 februari 2022
Antwoord
De 'kunst' is om het grootste gehele getal te zoeken waarmee je de teller en de noemer kunt delen. Dat heet de 'grootste gemene deler'. Op Breuken vereenvoudigen kan je dat vinden.
Je kunt ook de teller en noemer ontbinden in priemfactoren. Je kunt dan de gemeenschappelijke factoren wegdelen. Dat gaat zo:
\eqalign{\frac{{26}} {{36}} = \frac{{2 \cdot 13}} {{2 \cdot 2 \cdot 3 \cdot 3}} = \frac{{13}} {{2 \cdot 3 \cdot 3}} = \frac{{13}} {{18}}}
Lekker handig...
\eqalign{\frac{{34}} {{51}} = \frac{{2 \cdot 17}} {{3 \cdot 17}} = \frac{2} {3}}
Beter...
Nog maar een?
\eqalign{\frac{{15}} {{ - 21}} = - \frac{{3 \cdot 5}} {{3 \cdot 7}} = - \frac{5} {7}}
Ik weet niet welke rekenmachine je gebruikt maar met mijn CASIO kan ik de GGD uitrekenen. Dat scheelt dan weer...
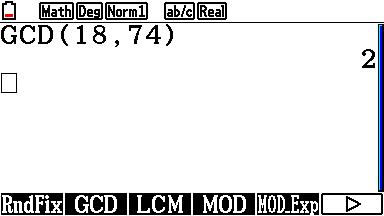
Kennelijk is \eqalign{ - \frac{{18}} {{74}} = - \frac{9} {{37}}} . Maar dan kan dan maar beter zo:
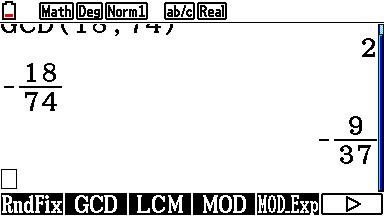
Op dezelfde manier geeft de laatste deze mogelijkheden:
\eqalign{\frac{{1008}} {{1080}} = \frac{{2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 7}} {{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 5}} = \frac{{2 \cdot 7}} {{3 \cdot 5}} = \frac{{14}} {{15}}}
Over handig gesproken... . Dan maar liever zo: . Dan maar liever zo:
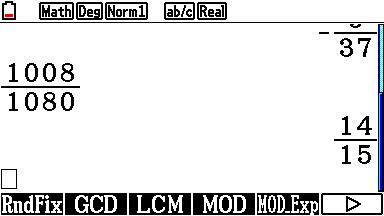
Dus kijk maar 's. Helpt dat?
Zie Grootste gemeenschappelijke deler

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 1 februari 2022
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|













