WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Horizontale raaklijn kromme

Beste

Ik zit even vast bij de volgende vraag, maar volgens mij is mijn werkwijze wel correct:

Gegeven is de volgende poolvergelijking van een kromme:

r = (sin(2t) - 1)·cos(t)

Gevraagd:
Bepaal de cartesische coordinaten met een horizontale raaklijn. Oplossing is (-1,1)

Mijn werkwijze:

Om een horizontale raaklijn te hebben moet dus gelden dat dy=0 en dx niet gelijk aan nul.

Ik heb deze poolvergelijking al omgezet in cartesische vergelijkingen:

X = rcost = (sin (2t) -1)cos²(t)
Y = rsint = (sin(2t)-1)cost.sint

Een probleem: als ik deze 2 uitdrukkingen afleid kom ik iets erg lang uit en kan ik het niet oplossen naar nul, dus hoe moet je het anders oplossen?

Alvast bedankt
Nvt
Student universiteit - maandag 3 januari 2022

Antwoord

Je kunt je $x$ en $y$ vooraf wat vereenvoudigen, bijvoorbeeld
$$y(t)=(\sin 2t-1)\cdot\frac12\sin2t=\frac12\sin^22t-\frac12\sin 2t
$$als je die differentieert komt er
$$y'(t)=2\sin2t\cdot\cos 2t -\cos 2t=(2\sin2t-1)\cos 2t
$$Daar zijn de nulpunten makkelijk van te bepalen.

Iets dergelijks kan met $x(t)$ ook: $\cos^2t=\frac12+\frac12\cos2t$
$$x(t)=\frac12(\sin2t-1)(\cos2t+1)
$$Probeer het maar.

Er zijn overigens meer oplossingen:

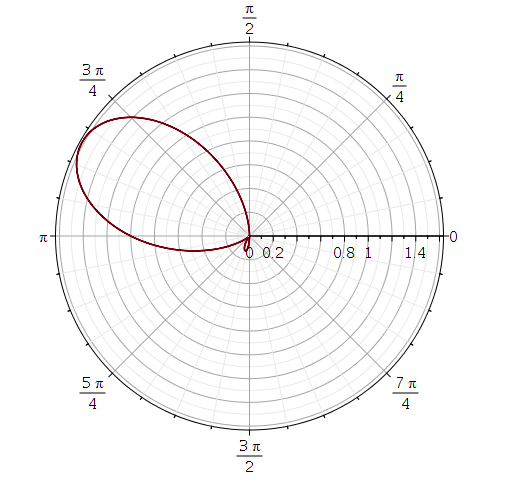
kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 3 januari 2022