WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Enquete, analyse van de data

Het opzetten van een enquete is dankzij de vele tips op dit bord niet zo moeilijk geweest.
Het probleem dient zich pas aan bij het verwerken van de gegevens.
Ik heb een formule gevonden waarmee je kan zeggen: met 95% zekerheid vindt men dit. (dit doe ik aan de hand van de schattingsfout). -- s=Ö((P*Q)/n)

Is er niet een formule waarmee je kan zeggen wat bijvoorbeeld geldt met 90% (of 85%) zekerheid.

Het gaat dus om de interpretatie van de gevonden resultaten, wat kunnen wij dus beweren als we vinden dat 47% van de mensen "ja" zegt op een vraag.
Moet hierbij nog verschil gemaakt worden tussen vragen en het aantal antwoordmogelijkheden?

De populatie is 108 en we hebben iedereen een enquete verstuurd. Tot nu toe zijn er 36 retour gekomen.
Tycho
Student hbo - maandag 31 maart 2003

Antwoord

Okay de populatie is 108 en er zijn dus geen anderen in die groep. Je hebt iedereen een enquete gestuurd. Dan hoef je feitelijk geen keuze te maken voor een steekproefgrootte. Nu is de vraag met welke onnauwkeurigheid ACHTERAF de uitspraken over fracties (percentages) gedaan kunnen worden.

welnu de formule daarvoor is:

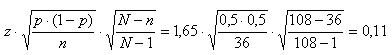
Betekent dat de onnauwkeurigheid in een percentageschatting +/-11% zal zijn

Enig commentaar hierop: N is de populatiegrootte en n is de steekproefgrootte
Ik heb als betrouwbaarheid genomen 90% in plaats van 95%. Het heeft namelijk niet zo heel veel zin om bij een kleine steekproef een hoge betrouwbaarheid te nemen omdat de onnauwkeurigheid nooit al te best is.
Deze formule geldt voor fracties, feitelijk zou je bij zo'n kleine steekproef nog wat correctietermen in de formule moeten gebruiken. Dat wordt te lastig.
Ook zou je bij kleine steekproeven moeten overwegen een continuiteitscorrectie in te bouwen. Ook dat is lastig en heb ik dus maar achterwege gelaten.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 1 april 2003

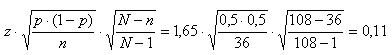
Re: Enquete, analyse van de data