WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Fabrieksverdeling

Een continue stochastische variabele X neemt waarden aan tussen 0 en 2.5. Zijn kansdichtheid is van de volgende vorm:
(zie plaatje)

We noemen dit de ‘fabrieksverdeling’, gekenmerkt door drie parameters:

$\to$ de totale breedte b van het gebouw: op de tekening is b = 2.5;
$\to$ de breedte van de schoorsteen bs: op de tekening is bs = 0.5;
$\to$ de hoogte van het gebouw h: op de tekening is h = 1/3.

a. Wat is de hoogte hs van de schoorsteen op de tekening op basis van een exacte berekening?

b. Veronderstel dat b en bs zijn zoals in de bovenstaande figuur, maar
dat je h nog niet kent. Bepaal dan h zodanig dat P(1,5 $\le$ X $\le$ 2,2) = 0,31

Voor a zou ik hs= ²/₃ moeten uitkomen en voor b: hs=0,8. Ik kom maar niet aan die oplossing terwijl ik het op verschillende manieren heb geprobeerd. Het spijt me voor dit blok tekst maar kan iemand mij aub helpen?
Elke
Student Hoger Onderwijs België - dinsdag 30 maart 2021

Antwoord

Graag laten zien wat je zelf geprobeerd hebt zodat we kunnen vaststellen waar het vast loopt.

Vraag a is in feite de opstap voor b. Dat wil zeggen dat je eerst vraag a goed moet begrijpen om vraag b te kunnen doorzien.

Vraag a is toch vrij eenvoudig wanneer je bedenkt dat de totale oppervlakte onder de kansdichtheidsfunctie 1 dient te zijn.

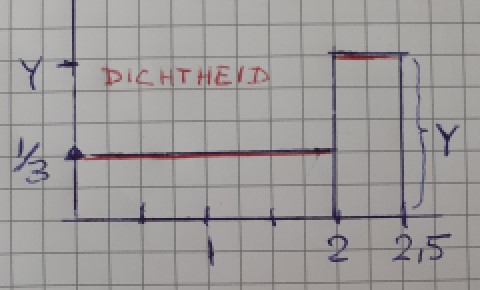
Hieruit is eenvoudig de hoogte Y (hs) te berekenen.

Als je dat dan hebt dan de volgende stap naar vraag b.

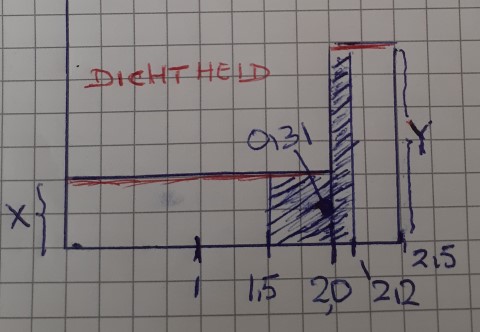
Hier gebruik je weer dat de oppervlakte onder de dichtheidsfunctie 1 dient te zijn. Dat leidt tot een vergelijking met twee onbekenden namelijk:
2X + 0,5Y = 1 (X=h, Y=hs)
Maar uit het gearceerde gebied tussen 1,5 en 2,2 valt nog een vergelijking met dezelfde twee onbekenden af te leiden.

Vervolgens heb je dan twee vergelijkingen met twee onbekenden en die kan je oplossen met resultaat Y=0,8

Succes,

Met vriendelijke groet
JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 30 maart 2021

Re: Fabrieksverdeling