WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hoekberekening

Ik wil een hoek berekenen van een kolom die horizontaal 11 graden verdraaid en verticaal 9 graden. Hoe pak ik dit aan met soscastoa
martin
Student hbo - woensdag 20 januari 2021

Antwoord

Hallo Martin,

Zeker bij ruimtelijke meetkunde is het van groot belang om je hoeken en assen goed te definiëren, zoals uit het volgende zal blijken:

Steek je rechter arm recht omhoog. Deze stelt een verticale kolom voor. Wat is nu horizontaal draaien? In het horizontale vlak, of rond een horizontale as?
Ik neem aan dat je rond een horizontale as wilt draaien, bijvoorbeeld rond een as van voor naar achter. Je arm is dan 11 graden naar buiten gedraaid. Vervolgens draai je je gehele lichaam 9 graden rond de verticale lengte-as. Nu wil je een(?) hoek weten. Welke hoek? De hoek tussen jouw arm en de verticaal is nog steeds 11 graden. Dat zal je niet bedoelen, maar wat dan wel?

Ook de volgorde is van belang, dat blijkt uit het volgende experiment:
Steek je rechter arm weer recht omhoog. Draai deze 90 graden rond een horizontale as die van schouder naar schouder loopt. Je arm wijst nu recht vooruit. Draai vervolgens 90 graden rond de verticale as. Nu wijst je arm recht opzij.
Nu gaan we de volgorde omdraaien. Steek je arm weer echt omhoog. Draai je arm (niet je lijf) nu eerst 90 graden om de verticale as. Je arm wijst nog steeds recht omhoog, alleen is nu je hand 90 graden gedraaid. Vervolgens draai je 90 graden rond de horizontale as door de schouders. Nu wijst je arm recht naar voren. Een geheel andere stand dus dan bij de eerste volgorde.

Kortom: begin met het definiëren van een assenstelsel: x-as, y-as en z-as, loodrecht op elkaar. Kies een rechtsdraaiend assenstelsel, dat wil zeggen: als je de positieve x-as in de richting van de positieve y-as draait, dan zou een rechtsdraaiende schroef in de richting van de positieve z-as bewegen. Dit is de gewoonte.
Geef dan duidelijk aan wat de uitgangspositie is van je kolom (ik vermoed verticaal, dus langs één van de assen). Geef dan aan rond welke assen je rotaties plaatsvinden, en in welke volgorde. Geef tot slot aan tussen welke twee lijnen/richtingen je de hoek wilt kennen. Wellicht kunnen we dan een antwoord geven.

Na insturen van plaatje:

Hallo Martin,

Je stuurde onderstaand plaatje van de situatie, ik heb hoekpunten benoemd van een balk waar de kolom zich in bevindt. Volgens dit plaatje zoek je de hoek CAG tussen het horizontale vlak en de lichaamsdiagonaal AG van de balk ABCD·EFGH. Dit is anders dan je in je tekst beschrijft. Ik ga uit van het plaatje.

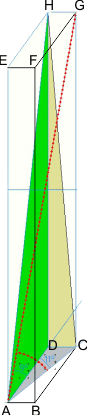
Je geeft aan:
Hoek DAG=9°
Hoek CAD=11°

Allereerst valt op dat je hoek DAH erg groot tekent t.o.v. de waarde 9°. Weet je zeker dat je niet bedoelt: Hoek EAH=9°?

Ik ga uit van het plaatje waarin je aangeeft Hoek DAH=9°. De gevraagde hoek CAG bereken je dan als volgt:

Stel AD=1 (In werkelijkheid hoeft dit niet zo te zijn. Dat maakt niet uit, het gaat alleen om verhoudingen). Dan geldt:

tan 9° = ^DH/₁, dus DH = tan 9° = 0,158...
Dan geldt ook: CG = 0,158...
tan 11° = ^CD/₁, dus CD = tan 11° = 0,194...

Met Pythagoras berekenen we AC:
AC = √(CD²+AD²) = √(0,194...²+1²) = 1,0187...

tan (hoek CAG) = ^0,158.../_1,0187... = 0,155...
hoek CAG = atan 0,155...° = 8,837...°.

Let op:
Ga nog eens goed na of je de gegevens op de juiste manier hebt doorgegeven (met name die hoek van 9°)
Ga nog eens goed na of de tekening werkelijk de gevraagde hoek weergeeft, deze stelt een andere situatie voor dan de beschrijving in je tekst.

Verder: stel een eventuele vervolgvraag via de website (zie de knop 'reageer' onder elk antwoord) en verwijs, indien van toepassing, naar een ingestuurd plaatje.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 23 januari 2021