|
|
|
\require{AMSmath}



Stelling van Pythagoras met dikte
Een schilderij is 2,20m x 2,20m x 5 cm (5cm is de dikte).
Kan je het schilderij door een deur (rechthoek) heen zetten als die 1m x 2m is?
En hoe bereken je dit?
Marcel
Leerling bovenbouw havo-vwo - woensdag 23 december 2020
Antwoord
Beste Marcel,
Als je het schilderij op zijn kant door de deur gaat proberen te krijgen, dan gaat het dus eigenlijk om een rechthoek van 220 cm x 5 cm die door een rechthoek van 100 cm x 200 cm moet passen.
De diameter van de "schilderijrechthoek" is $\sqrt{48425}$ cm met behulp van Pythagoras. Als het schilderij precies past door de deur, dan raakt hij de onderkant en bovenkant van de deuropening op gelijke afstanden van de zijkant, zeg $x$, en hij raakt de zijkanten op gelijke afstanden van de boven en onderkant, zeg $y$. Zie figuur.
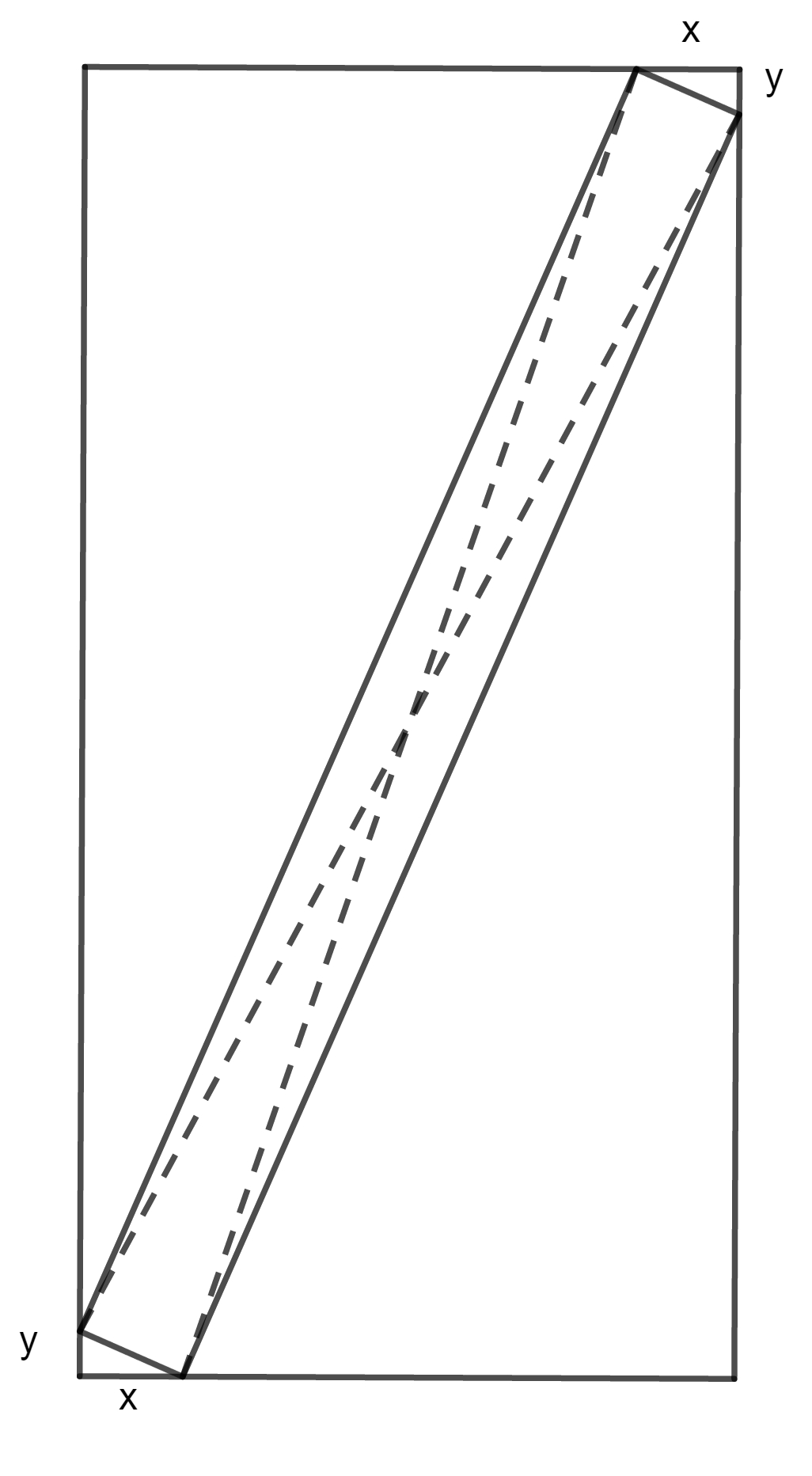
Met Pythagoras zie je nu dat (in cm) $(100-2x)^2+200^2=48425$ waaruit je $x$ kunt bepalen. Evenzo kun je $y$ bepalen uit $100^2 + (200-2y)^2=48425$. Vervolgens kun je checken of $x^2+y^2$ voldoende is voor die 5 cm breedte.
Succes!
Met vriendelijke groet,

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 23 december 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|










