WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Wat is breuksplitsen?

Hallo,

Ik heb een voorbeeld gevonden op internet van breuksplitsen alleen ik snap het niet helemaal. Ik zal het voorbeeld even geven:

(x-1)/((x+3)(x²+3x+2)) deze breuk moet gesplitst worden
dan doen ze:

(x-1)/((x+3)(x²+3x+2)) = A/(x+3) + (Bx+C)/(x²+3x+2) ik snap niet waarom ze dit doen. Kunt u mij dit uitleggen?

Dan gaan ze verder met:

x-1 = A(x²+3x+2) + (Bx+C)(x+3)dit snap ik weer
dan vullen ze x=-3 in en hiermee berekenen ze dat A=-2, dit snap ik.

0 = A+B ik snap niet hoe ze hier aan komen, kunt u me dit ook uitleggen?

Dan gaan ze verder:

0 = -2 + B
2 = B dit snap ik
Dan gaan ze verder:
1 = 3A + 3B + C ik snap niet hoe ze hier aan komen, kunt u me dit ook uitleggen?
1 = 3(-2) + 3(2) +C
1 = C dit snap ik wel
de uitkomst wordt dan:

(x-1)/((x+3)(x²+3x+2)) = -2/(x+3) + (2x+1)/(x²+3x+2)

Ik hoop dat u antwoord kunt geven op mijn vragen, alvast bedankt.

Groetjes Elsbeth
Elsbet
Leerling bovenbouw havo-vwo - donderdag 27 maart 2003

Antwoord

Beste Elsbeth,

Breuksplitsen is eigenlijk het tegenovergestelde van breuken onder één noemer brengen. Dus algemeen geldt voor breuken dat:

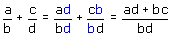
Hetzelfde geldt als je niet onbekenden in de noemer en teller hebt staan maar "vergelijkingen". We zoeken dus

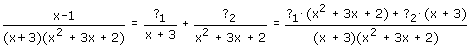
Dit is een beetje intuitief opgeschreven; je moet nu gaan bedenken hoe ?₁ en ?₂ er ongeveer uit zouden moeten zien.
Je ziet al dat: ?₁·(x²+3x+2)+?₂·(x+3) = x-1

Dus ?₁ zal wel een getal zijn (zeg A), aan de rechterkant van het = teken is de hoogste macht x. Aan de linker kant staat dan zeker een x² door de vermenigvulding met x²+3x+2. Die moet je weer weg zien te krijgen want die staat niet aan de rechterkant. De enige mogelijkheid is die er weer af te trekken. Dat lukt als we x+3 vermenigvuldigen met Bx + C.
Het is dus een beetje op gevoel werken, maar zo zijn ze dus aan die A en Bx+C gekomen.

Je zegt dat je dan al begrijpt dat:
x-1 = A(x²+3x+2) + (Bx+C)(x+3)

Werk dit maar eens uit:

x-1 = Ax²+3Ax+2A+Bx²+3Bx+Cx+3C = (A+B)x²+(3A+3B+C)x+2A+3C

Dus:
(A+B)=0
(3A+3B+C)=1
2A+3C = -1

Vul je de eerste vergelijking 3 keer in de tweede in dat vindt je dat C = 1
Vul je C =1 in de derde vergelijking in dan vind je dat A = -2 en vul je dit weer in de eerste in dan vind je dat B =2.

Misschien vind je deze methode makkelijker dan het voorbeeld dat je gaf.

Ik hoop dat het nu duidelijk is. Zo niet laat het dan even weten en dan proberen we het op een andere manier uit te leggen.

Zie ook Breuksplitsen

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 29 maart 2003

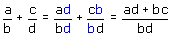
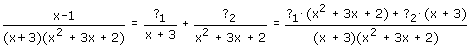
Breuksplitsen