WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Goniometrische vraag met arccos en pi

Ik ben tijdens het maken van een paar opdrachten op deze vraag gestuit. Dit is kennelijk een kernvraag, want de vragen erna zijn net zo. Als ik deze begrijp, begrijp ik de rest ook. Ik zou jullie dankbaar zijn als jullie kunnen helpen.

De vraag is:

Bepaal de uitkomst(en) van a = arccos(cos(6p / 4)

Alvast bedankt!
mvg
Ryoga
Ryoga
Student hbo - donderdag 27 maart 2003

Antwoord

Beste Ryoga,

Eerst moet je weten dat de arccos-functie betekent "de inverse functie van de cosinus" (zoals worteltrekken en kwadrateren inverse bewerkingen zijn, je kunt met de arccos berekenen van welke waarde de cosinus genomen moet worden zodat een vooropgestelde uitkomst wordt bereikt).
Bijvoorbeeld: arccos(¹/₆p) 1,019726743 dus cos(1,019726743) ¹/₆p.

In jouw voorbeeld. a = arccos(cos(1¹/₂p))
Eerst moet je berekenen wat cos(1¹/₂p) is. Dat kun je met je rekenmachine doen, maar ook als je de cosinusfunctie voor de geest haalt.

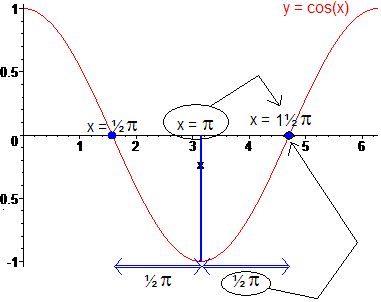
Dus voor x = 1¹/₂p is de cosinusfunctie 0.
Maar je moest hebben arccos(cos(1¹/₂p)), dus arccos(0).
Je vraagt je dus eigenlijk af voor welke waardes is de cosinus functie 0? Oftewel voor welke x-waardes geldt dat cos(x) = 0. Zoals in bovenstaande plot volgt daar uit, x = ¹/₂p, x = 1¹/₂p, x = 2¹/₂p, ... (komt telkens p bij), maar dit geldt ook in 't negatieve (dus ook voor x = -¹/₂p, x = -1¹/₂p, ... (telkens p ervan af)). Oftewel algemeen cos(x) = 0 Û x = ¹/₂p + kp (met k Î ).

Groetjes,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 27 maart 2003