|
|
|
\require{AMSmath}
Re: Spiegeling parabool op een punt
Dank U klaas Pieter, voor dit inzicht in spiegelingen. Het is klaar en duidelijk voor dit geval .
Maar neem ik nu een vergelijking P(1): y=x2 en P(1) is dan het beeld door het punt (-1;2).Hoe kom ik dan aan y=-x2-4x
Het spiegelen van x naar -x en dan het kwadraat nemen volgens de geven functie neem ik wel aan .Maar dan nog -4x daarachter. Graag nog wat uitleg over hoe er moet geredeneerd worden om die spiegeling goed af te werken...
Groetjes
Rik
Rik Le
Iets anders - vrijdag 9 oktober 2020
Antwoord
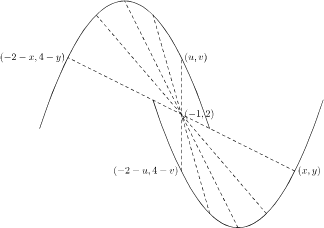
Het gaat net als de vorige keer: wel opletten dat $x$ om $-1$ gespiegeld wordt en $y$ om $2$. Dus $(x,y)\mapsto(-2-x,4-y)$.
Via $(u,v)$ vinden we dat $4-v=(-2-u)^2$; dat kun je omwerken tot $v=4-(2+u)^2$ of $v=-4u-u^2$.
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 9 oktober 2020
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 90630