WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Een lichaam

Kan iemand mij helpen bij a en b (b is voor mij nog ingewikkelder.

Het antwoord van a:
1) is door O // AC
2) door O//AB
...wat niet helemaal duidelijk is.

In R³ is gegeven het lichaam OABC (zie figuur 95)

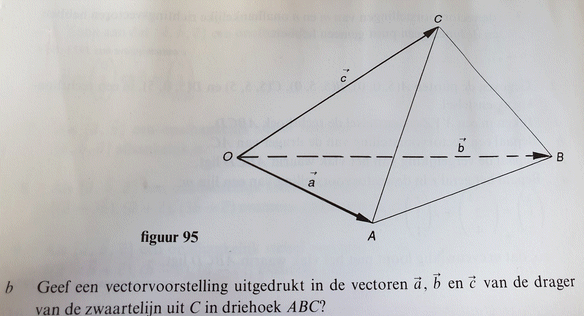
a. Welke lijn of welk vlak wordt voorgesteld door:
1) v=l(a-c)
2) v=ma+wb?
b. Geef een vectorvoorstelling uitgedrukt in a,b en c van de drager van de zwaartelijn uit C in driehoek ABC.
mboudd
Leerling mbo - woensdag 12 februari 2020

Antwoord

Hallo Mboudd,

vraag a.
Algemeen is de vorm van een lijn $\vec{v} = \vec{s} +\lambda\vec{r}$. Daarin is $\vec{s}$ de steunvector, die je wijst naar een "beginpunt". En $\vec{r}$ is de richtingsvector. Het woord zegt het al, die geeft de richting aan van de lijn. Elk punt op de lijn vind je vanuit $O$ door eerst via de steunvector naar het beginpunt te gaan, en dan een aantal ($\lambda$) keer de richtingsvector af te volgen.

1) Lees ik hem goed als $\vec{v} = \lambda(\vec{a}-\vec{c})$? Dan is dit een lijn met de nulvector als steunvector, dus de lijn gaat door $O$. En de richtingsvector is $\vec{a}-\vec{c} = \overrightarrow{CA}$.

2) Ik lees iets als $\vec{v} = \mu\vec{a}+\omega\vec{b}$. Dat komt niet overeen met het antwoord, want dit zou twee richtingsvectoren opleveren en dan krijg je een vlak.

b. De gevraagde zwaartelijn loopt van $C$ naar het midden van $AB$, zeg $M$. De steunvector is hier wel duidelijk denk ik, dat is $\vec{c}$. Voor de richtingsvector kunnen we $\overrightarrow{CM}$ nemen. De plaatsvector $M$ van $AB$ is $\vec{m}=\frac12 (\vec{a}+\vec{b})$. Dus krijg je $\overrightarrow{CM}=\vec{m}-\vec{c}$. Maak jij het af?

Met vriendelijke groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 12 februari 2020

Re: Een lichaam