WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Een parallellogram

Dit is een reactie op vraag 88922

Dankuwel voor de uitgebreidere uitleg. Alleen één vraag voor de vectoren AC en BD. Waarom kan AC niet a-c zijn ipv c-a en BD niet b-d? Ik zie toch dat dat dezelfde representatieven zijn. Ik heb nu wel een goede tekening opgestuurd.
mboudd
Leerling mbo - donderdag 2 januari 2020

Antwoord

Hallo,
In het pdf-bestand moet het antwoord op je vraag toch ook wel te vinden zijn, denk ik. Maar hieronder laat ik zien dat een en ander ook volgens de diagonaalmethode klopt.
Ik teken dus de vector(van A naar C), die begint in A en eindigt met een pijl in C.

Ik bewijs dus, dat de vector(van A naar C) $=\vec{AC}= \vec{c} - \vec{a}$.
En NIET andersom.

In de linker figuur hieronder staat de uitgangspositie, die ongeveer overeenkomt met het plaatje dat je stuurde.

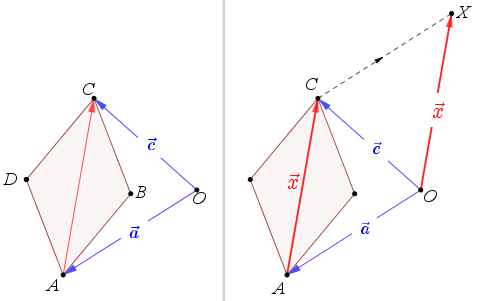
Je weet dat je vrije vectoren evenwijdig mag verplaatsen. Dat doe ik dus met de vrije vector $\vec{AC} = \vec{x}$: punt A gaat naar O, punt C gaat naar X.
Zie dan de rechter figuur. Daarin is nu ook $\vec{OX} = \vec{x}$.
En, vierhoek AOXC is een parallellogram.
Volgens de optelling met de diagonaalmethode is daarin:
$\vec{OA}+\vec{OX} = \vec{OC}$, zodat $\vec{a} + \vec{x} = \vec{c}$
En omdat we $\vec{x}$ willen weten, moet gelden ($\vec{a}$ aan beide kanten aftrekken):
$\vec{x} = \vec{c} - \vec{a}$
Duidelijk toch?

Merk op dat rechts volgens kop-staart geldt (van O via A naar C):
$\vec{a} +\vec{x} = \vec{c}$, zodat ook hier: $\vec{x} = \vec{c} - \vec{a}$
En dan is natuurlijk ook:
de vrije vector(van B naar D) $=\vec{BD}=\vec{d}-\vec{b}$ (en niet andersom!)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 2 januari 2020

Re: Re: Re: Een parallellogram