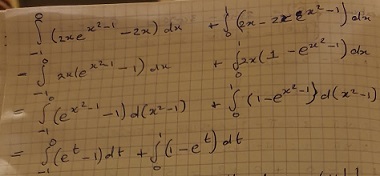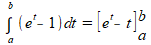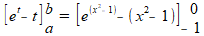|
|
|
\require{AMSmath}
Re: Oppervlakte tussen een lijn en e-functie
Ok dat is gelukt alleen bij het berekenen van de integraal kom ik wanhopig in de knoei ik heb mijn uitwerking opgestuurd.
Mboudd
Leerling mbo - vrijdag 20 december 2019
Antwoord
Tot hier gaat het grotendeels goed:
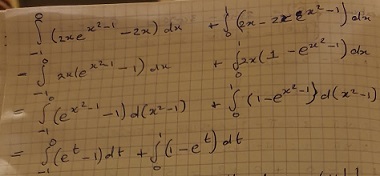
Bedenk alleen dat de grenzen voor integratie -1 tot 0 en 0 tot 1 gelden voor x, niet voor t. In de onderste regel mag je deze grenzen dus niet bij het integraalteken zetten. Je zou hier de bijbehorende waarden voor t moeten noteren. Na integreren ga je weer terug naar x in plaats van t, dan mag je deze grenzen weer wel hanteren.
Het primitiveren gaat mis. Dit is de juiste uitwerking (voor de linker integraal):
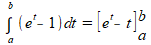
Voor a en b zou je de waarden moeten berekenen die t aanneemt bij x=-1 en x=0. Maar deze hebben we niet echt nodig, want bij de volgende stap substitueer je weer terug naar x. Dan ga je ook weer over naar de grenzen van x:
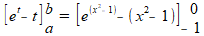
Nu weer zorgvuldig invullen en verder uitwerken.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 21 december 2019
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 88865 