WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Formule voor een rij

Geachte Dames en Heren,
Ben al héél lang van school en hoop dat u mij toch wilt helpen.

Wat ik zoek kan ik uiteraard wel 'normaal' uitrekenen, maar ik hoop dat er:
Ook een formule bestaat en welke is dat en hoe heet die formule?
En als er andere tekens in voorkomen dan simpel +,-, :, x, kunt u dan erbij schrijven wat ze betekenen en hoe ik dat teken moet uitspreken?
Misschien bestaat er ook een lijst met al die voor mij nieuwe tekens?
Ben vooral nieuwsgierig naar betekenis van een soort golvendteken, wat is dat?
Dit is de (versimpelde) vraag:

Ik start met E 100,- en geef 10% uit; vervolgens van die overgebleven E 90,- weer 10%, en van de E 81, weer 10% enz.

5. Stel dat ik dat 10x doe,
- hoeveel Euro is dan de laatste afromende 10%
- en wat is dan het bedrag van de laatste overblijvende 90%
- en hoe bereken ik dat?
- is daar een formule voor en hoe heet die?

6. En wat is de som
- van al die 10 10% bedragen
- en wat is dan de som van alle 90% bedragen ?
- is daar een formule voor?
- en hoe heet die?

Hoop dat u tijd heeft om mijn vraagjes te beantwoorden: bij voorbaat vriendelijk dank
Zon Da
Iets anders - zaterdag 14 december 2019

Antwoord

Bij 5.

De formule is:

$B=100\times0,9^t$

met $B$=bedrag en $t$=tijd.

Het voorlaatste bedrag is $B=100\times0,9^9\approx38,74$ en het laatste bedrag is $B=100\times0,9^{10}\approx34,87$. De laatste 'afromende 10%' is $3,87$.

Je hebt hier te maken met exponentiële groei. Je rekent daarbij met groeifactoren. Je kunt vermenigvuldigen met $0,9$ beschouwen als '10% er af'.

Het is ook een voorbeeld van een meetkundige rij. De 'reden' is gelijk aan $0,9$ en de startwaarde is $100$:

In het algemeen geldt voor de som van een meetkundige rij:

$
\eqalign{S_n = \frac{{{\text{volgende}} - {\text{eerste}}}}
{{{\text{reden}} - 1}}}
$

In dit geval:

$
\eqalign{S_{10} = \frac{{100 \times 0,9^{11} - 100}}
{{0,9 - 1}} \approx {\text{686}}{\text{,19}}}
$

Ik heb 't ook maar 's in Excel gezet:

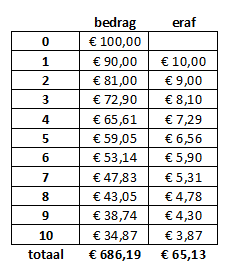
...en het klopt...

Op wiskundige symbolen kan je nog de betekenis vinden van een aantal veelgebruikte wiskunde symbolen.
Zie eventueel ook Wat zijn machten?
Meer basiskennis op Snippers
Hopelijk kan je er mee verder.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 15 december 2019