WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Transformaties bij verschillende vormen

Hoi,

Mijn naam is Sandra en ik ben bezig met een werkstuk over Escher. Nu ben ik bijna klaar, alleen is er een probleem waar ik telkens over struikel. Ik moet uitleggen waarom bepaalde transformaties bij bepaalde vormen wel/niet kunnen en waarom. Zoals, bijvoorbeeld, een translatie bij alle vormen behalve een driehoek kan- ik moet uitleggen waarom. Kun je me misschien helpen bij deze vlakvullingen?

Groetjes,
Sandra
Sandra
Leerling bovenbouw havo-vwo - zaterdag 22 maart 2003

Antwoord

We houden het (vooralsnog) even bij vlakvullingen met regelmatige veelhoeken.
Wat bepaalt nu (onder andere) zo'n vulling?
In ieder geval moeten de gebruikte congruente figuren bij een hoekpunt aan elkaar sluiten.
Dus SAMEN een hoek van 360 graden vormen.
Bekijken we opvolgend de hoeken van de "eerste" regelmatige veelhoeken.
Regelmatige driehoek: 60 graden. Gelukkig is 60 een deler van 360, dus we hebben er 6 nodig.
Regelmatige vierhoek: 90 graden; benodigd vier stuks.
Regelmatige vijfhoek: 108 graden; twee is te weinig; drie is te veel.
Regelmatige zeshoek: 120 graden; drie!
Regelmatige zevenhoek: met (5 x 180)/7 graden dat gaat niet lukken.
Regelmatige achthoek: 135 graden; lukt ook niet.
En verder hoeven we niet te proberen ...
Het kan dus alleen met regelmatige drie-, vier- en zeshoeken (zoals trouwens de oude Grieken reeds wisten).

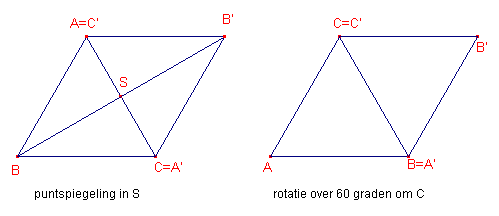
Als je via een congruentie-transformatie (rotatie, translatie, spiegeling) drie (regelmatige) driehoeken "rondom" een hoekpunt wil krijgen, dan kan je toepassen:
puntspiegeling in het midden van een zijde;
In dit geval ontstaat er een ruit (parallellogram), die (dat) weer kan dienen om met translaties "stroken" te maken.
rotatie om een hoekpunt over 60 graden; en dit geeft dezelfde figuur.
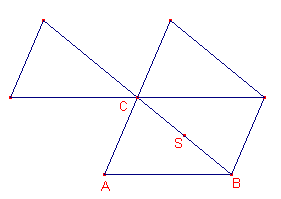
Ga je uit van niet-regelmatige (convexe) veelhoeken, dan wordt het een stuk gecompliceerder.
Bij een driehoek lukt het wel weer via een puntspiegeling in het midden van een zijde; je krijgt dan weer een parallellogram.
Overigens, hier kunnen we door elk van de hoeken van de driehoek dubbel rondom dat hoekpunt te plaatsen, tot een totaal van 360 graden komen.
En ook bij een vierhoek lukt het wel; weer door middel van een puntspiegeling. Je krijgt dan een zeshoek waarvan de zijden twee aan twee evenwijdig zijn.

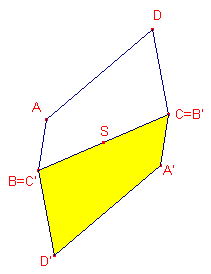
En voor de rest wordt het nogal ingewikkeld.
In 1918 beschreef K. Reinhart in zijn proefschrift aan de Universiteit van Frankfurt hoe het echt allemaal zit met een niet-regelmatige zeshoek (hoewel...).
Van 1967-1969 (ja toen pas) werd alles netjes op een rijtje gezet door Richard Kershner (Hopkins Universiteit).
Kershner onderscheidde acht gevallen (drie meer dan Reinhart!).
En in 1975 bleek dat Kershner er toch eentje gemist had.
Deze zeshoek (gevonden door Richard E. James III, een computerwetenschapper) voldoet aan:
A = 90; C + D = 270; 2D + E = 2C + B = 360, waarbij verder a = b = c + e.

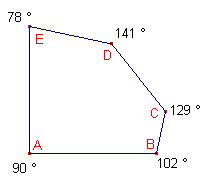
Het is allemaal dus niet zo eenvoudig!
Maar probeer zelf eens met de laatste twee figuren een vlakvulling te maken!
Zie MathWorld - Tiling

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 23 maart 2003