|
|
|
\require{AMSmath}
Re: Re: Vectoren
Dank je wel. Heb dit ook al beredeneerd en precies tot zelfde tekening gekomen, maar heb dan een rechthoek geplooid en op een kubus gelegd.
(RP) = aan vierkantswortel ( (XP)2 + (XR)2).
X zal per definitie rechte hoek hebben in driehoek RXP, maar niet in driehoeken EXP, XPF, FXR en EXR.
Heb A4-tje genomen en dit op een kubus gelegd om te visualiseren.
Dus als EXP geen rechthoekige driehoek zou zijn, dan is (XP) niet te berekenen met Pyth.
Heb ook al gedacht aan stelling dat PR = 2 x Z1Z2, met Z1 het zwaartepunt van driehoek EFP en Z2 het zwtpnt van driehoek EFR. Helaas ook hier heb ik geen idee hoe ik de afstand Z1Z2 kan berekenen.
Ik denk dat ik iets fundamenteels over het hoofd zie inzake eigenschappen van tetraeder of van de zwaartepunten...
kkel
3de graad ASO - zondag 29 september 2019
Antwoord
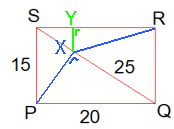
$XP$ is de hoogtelijn van de rechthoekige driehoek EPF, dus dat is te doen. Ik kom op $PX=12$ en $SX=9$. Mooier wordt het niet. Zou de rest dan ook lukken?
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 29 september 2019
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 88514