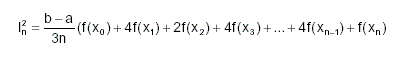Natuurlijk moet je beginnen met het uitleggen hoe deze regel van Simpson werkt. Wellicht wil je daarbij ook iets over de trapeziumregel zeggen (waarvan de regel van Simpson als een verbetering gezien kan worden).
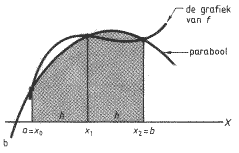
De regel van Simpson geeft een numerieke benadering van een integraal (=0ppervlakte onder een grafiek). Deze benadering wordt verkregen door telkens kleine stukjes van de grafiek te benaderen met een stukje parabool (bij de trapeziumregel benader je met een stukje rechte). Het voordeel van die parabool is dat je de kromming van de grafiek ook inbouwt. Nu is de benadering van de grafiek in de bovenstaande tekening niet erg nauwkeurig. Dat komt omdat je opppervlakte boven het interval [a,b] in een stap probeert te benaderen. Veel beter kun je telkens een klein stukje van de oppervlakte onder de grafiek benaderen. We spreken dan van de herhaalde Simpson-regel.
De bovenstaande figuur geeft wel aan wat er nodig is. Voor het bepalen van een passend paraboolstuk zijn per benadering 3 punten nodig, 3 punten bepalen namelijk de loop van een parabool. Vandaar dat we bij deze methode straks het interval in n stukjes gaan verdelen waarbij n EVEN moet zijn. Dat garandeert dat we naast een beginpunt en een eindpunt voor benadering ook telkens een tussenpunt voor de parabool kunnen vinden.
De afleiding van de formules lijkt voor Havo-Vwo te hoog gegrepen. Overweeg om dit deel niet te behandelen.
De formule van de formule van Simpson is als volgt:
Zij het interval [a,b] verdeeld in n (EVEN) gelijke delen met grenswaarden
a = x0, x1, x2,.....,xn-1, xn = b
dan a$\int{}$bf(x)dx = 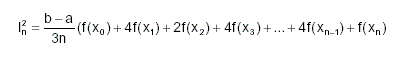
Die 2 in I2 verwijst naar de tweedegraads benadering volgens Simpson, het betekent niet dat je in de berekening daar een extra kwadraat krijgt. Achteraan moet nog een ) toegevoegd worden.
Laten we eens kijken naar een voorbeeld.
Bereken 1$\int{}$21/x dx (de uitkomst is natuurlijk ln 2, ga dat zelf na).
We verdelen [1,2] in 8 stukken. Dan wordt de benadering:
I8=(1/24)·[1/1,0 + 4/1,125 + 2/1,250 + 4/1,375 + 2/1,5 + 4/1,625 + 2/1,75 + 4/1,1875 + 1/2,0] = 0,6931545
Kunnen we nu ook iets zeggen over de maximale fout in deze schatting? Dat kan (wederom is de afleiding redelijk lastig en in ieder geval een heel verhaal).

In het voorbeeld is die M4= het maximum van de absolute waarde van de vierde afgeleide van f(x) op [1,2].
Die vierde afgeleide van f(x)=1/x lukt je vast wel (4 maal differentieren). Laat dan zien dat M4=24. De maximale fout En in de schatting kun je vervolgens ook zelf wel berekenen...... en eh..... je weet ook wat ln 2 is.... laat t.z.t. maar eens horen hoe die presentatie verlopen is.
Met vriendelijke groet
JaDeX