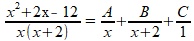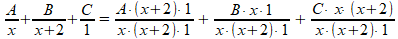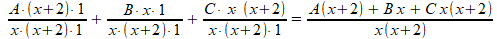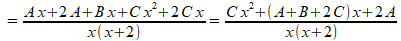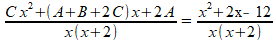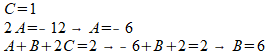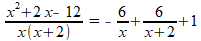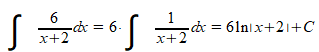WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Breuksplitsing?

Dit is een reactie op vraag 88324

Goede morgen en week Gilbert,

De omkering van de coëfficiënt in de noemer die vervolgens als constante wordt geplaatst voor het integraalteken dat begrijp ik nog wel maar bij de splitsing van de resterende breuk in drie(?) breukjes met constante tellers, kan ik 't helaas niet meer volgen.

Uw stapsgewijze uitwerking daarvan wordt op hoge prijs gesteld.
Hoe kan overigens het vormpje
  6
-----
x + 2
worden geprimitiveerd?
Adriaa
Ouder - zondag 28 juli 2019

Antwoord

Hallo Adriaan,

Het is niet noodzakelijk om de constante factor 1/3 voor het integraalteken te plaatsen, maar ik vind het overzichtelijker rekenen.

Het breuksplitsen gaat als volgt. We zoeken constanten A, B en C zodat geldt:

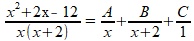
Dit doen we door 'terugrekenen' van het rechterlid: we tellen de breuken op en zorgen er achteraf voor dat de constanten A, B en C kloppen.
Om de breuken op te tellen, maken we eerst de noemers gelijk:

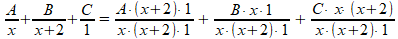
Vervolgens tellen we de breuken bij elkaar op:

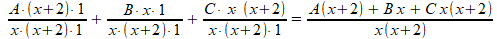
In de teller haakjes wegwerken en sorteren:

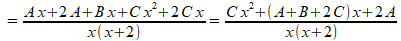
Het resultaat moet gelijk zijn aan de oorspronkelijke breuk:

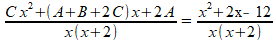
We vinden:

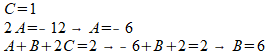
De gevonden waarden voor A, B en C invullen levert:

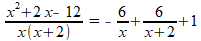
Tot slot: voor het primitiveren van de vorm 6/(x+2) brengen we eerst de constante factor 6 buiten de integraal, we houden een standaard integraal over (zie Wikipedia: Lijst van integralen):

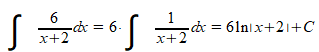
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 29 juli 2019