WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Normale verdeling

Het vraagstuk gaat als volgt: ‘Als Thomas om 7:50 u naar school vertrekt dan komt hij in 4% van de gevallen te laat als de les om 8:30 begint maar als hij om 7:45u vertrket komt hij maar in 1% van de gevallen te laat. De reistijd is normaal verdeeld. Om hoe laat moet hij vertrekken om in niet meer dan 0,5 % te laat te komen.’ Ik veronderstel dat je de verwachtingswaarde en de standaardafwijking moet berekenen maar ik weet niet hoe ik hier aan moet beginnen.
Laura
3de graad ASO - zaterdag 15 juni 2019

Antwoord

Hallo Laura,

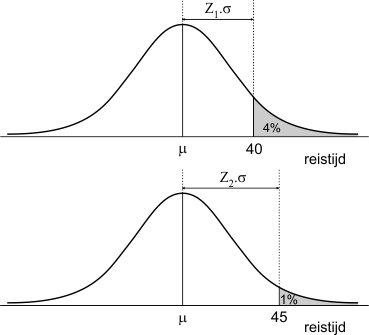
Om overzicht te krijgen over de situatie, is het handig om de gegevens in een schets weer te geven. De reistijd is normaal verdeeld. We kunnen dus de normaalkromme voor de reistijd schetsen, alleen weten we de waarde voor het gemiddelde $\mu$ en de standaardafwijking $\sigma$ nog niet. Wel weten we dat:
4% van de reizen duurt langer dan 40 minuten,
1% van de reizen duurt langer dan 45 minuten.
In onze schets ziet dat er zo uit:

Elke waarde X van de reistijd kent een zgn. Z-score, deze geeft aan hoeveel keer de standaardafwijking de waarde van X verwijderd is van het gemiddelde. Voor X geldt dus:

X = $\mu$ + Z·$\sigma$

Hoe verder de waarde X verwijderd is van $\mu$, hoe groter Z wordt. Bij elke waarde van Z hoort een vaste waarde (percentage) van de oppervlakte onder de normaalkromme links van deze waarde, en dus ook rechts.
Ons eerste gegeven is: 4% van de oppervlakte ligt rechts van de waarde '40', dus 96% ligt links van '40'. De bijbehorende waarde van Z vinden we uit de standaard-normaalverdeling ($\mu$=0, $\sigma$=1). Voor deze standaard-normaalverdeling bestaan tabellen, of je gebruikt je (grafische) rekenmachine. Op mijn rekenmachine gebruik ik de functie 'InvNorm', met Opp=0,96; $\mu$=0, $\sigma$=1. Je kunt ook dit hulpje gebruiken (Vul 0.96 in bij P(X $<$ ....) en klik op $<$--):

Je vindt: Z₁=1,751
dus:
$\mu$ + 1,751·$\sigma$ = 40
Op dezelfde wijze vindt je voor het gegeven '1% van de oppervlakte ligt rechts van '45': Z₂=2,326
dus:
$\mu$ + 2,326·$\sigma$ = 45
Je hebt nu twee vergelijkingen met twee onbekenden, $\mu$ en $\sigma$. Je kunt deze nu dus berekenen. Wanneer je $\mu$ en $\sigma$ eenmaal kent, dan kan je ook de reistijd berekenen die in slechts 0,5% van de gevallen wordt overschreden.

Kan je hiermee verder?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 16 juni 2019