WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Afstand tussen punt P op een kegel tot de top

In een opgave van het boek Getal en ruimte 3H1 hoofdstuk 4 wordt een aantal cirkels getekend die ( denkbeeldig ) op elkaar staan, zodat een kegel ontstaat. De afstand van de top T tot het grondvlak is hierbij 16 cm. Er zijn 4 cirkels op elkaar geplaatst en de afstand tussen deze cirkels is telkens 4 cm, waarbij de afstand van de kleinste cirkel tot de buitenste cirkel, die het grondvlak vormt, dus 16 cm is. De diameter van de buitenste cirkel is 16 cm.

De vraag is: Bereken in cm nauwkeurig de afstand van het punt P op de buitenste cirkel tot de top.

Ik heb dit als volgt aangepakt:

De afstand van het midden van de kegel tot aan de top is 16 cm. De diagonaal is 16 cm, dus de straal is 8 cm. Dus TP² = 16² + 8². Dus TP² = 320. Dus TP = 320^0,5 = 17,9 cm.

Het antwoordboekje geeft echter 18,9. Ik vraag me af welke denkfout ik hier maak.
Joost
Iets anders - vrijdag 4 januari 2019

Antwoord

Hallo Joost,

Je vraag is niet helemaal duidelijk. Je zegt dat er 4 cirkels boven elkaar zijn, met steeds 4 cm tussen deze cirkels. Dan zijn er 3 tussenruimtes, zodat de afstand tussen de bovenste en onderste cirkel 3x4=12 cm is, niet 16.

Kan het zijn dat je eigenlijk schijven bedoelt, en dat het om de kegel gaat zoals in onderstaande figuur?

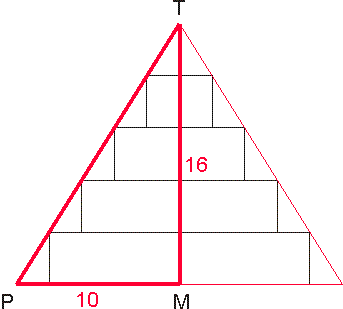
Wanneer de diameter van de onderste schijf 8 cm is, dan is de afstand PM 10 cm. Met een hoogte MT=16 cm vind je met jouw berekening: PT=18,9 cm.

Als het anders is, geef dan een betere beschrijving van de opgave, of stuur een plaatje naar plaatjes@wisfaq.nl.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 4 januari 2019

Re: Afstand tussen punt P op een kegel tot de top