|
|
|
\require{AMSmath}
Booglengte berekening
hoe bereken ik de booglengte als y=¦(x) y=1/2x2-1/4ln(x)met de booglengte formule 2$\int{}$x=1√1+(¦')2
henk
Student hbo - dinsdag 18 maart 2003
Antwoord
Beste Henk,
De formule voor de booglengte is
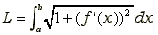
en deze moet een onder- en een bovengrens hebben. Je moet dus weten op welk interval je de lengte van de functie f(x) = 1/2x2 - 1/4ln(x) moet gaan berekenen (meestal is dat benaderen, want ingewikkelde wortelfuncties zijn zéér moeilijk exact te integreren. Je kunt dus het beste gebruik maken van je grafisch rekenmachine of een algebraïsch softwarepakket).
Ik zal je de afgeleide van f(x) = 1/2x2 - 1/4ln(x) geven, dan kun je zelf de lengte gaan benaderen (want je hebt het integratie-interval niet gegeven).
f'(x) = (1/2x2)' - (1/4ln(x))' afgeleide van een verschilfunctie
f'(x) = 1/2(x2)' - 1/4(ln(x))' constanten vooropzetten
f'(x) = 1/2·(2x) - 1/4·(1/x) standaardafg.
f'(x) = x - (1/(4x)) breuken vermenig.
f'(x) = (4x2 - 1)/(4x) één breuk maken
Þ (f'(x))2 = ((4x2 - 1)/(4x))2
= (4x2 - 1)2/(4x)2
De teller is van de vorm (a-b)2 = a2 - 2ab + b2 (merkwaardig product) en de noemer is van de vorm (ab)2 = a2b2.
= ((4x2)2 - 2(4x2·1) + 1) / (16x2) = (16x4 - 8x2 + 1) / (16x2) = x2 - 1/2 + 1/16x2 (dit laatste heb ik gekregen door alle termen te delen door 16x2).
aòb =  ( 1 + x2 - 1/2 + 1/16x2)
aòb = ( x2 + 1/16x2 + 1/2)
Duidelijk?
Groetjes,
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 19 maart 2003
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
