WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Cirkels

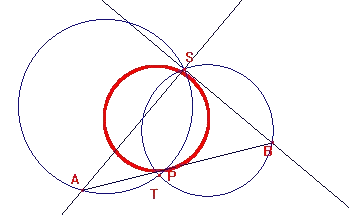
Twee cirkels 𝑐1 en 𝑐2 snijden elkaar in 𝑆 en 𝑇. Lijn 𝑎 snijdt 𝑐1 in 𝑆 en 𝐴. Lijn 𝑏 snijdt 𝑐2 in 𝑆 en 𝐵. De lijnen 𝑎 en 𝑏 staan loodrecht op elkaar. Punt 𝑃 is het midden van 𝐴𝐵. Wat is de meetkundige plaats van 𝑃? Bewijs dit.

Iemand enig idee... Ik zie het niet?
Tanja
Student hbo - zaterdag 3 november 2018

Antwoord

Beste Tanja,

Merk op dat $PA=PB=PS$.
Het middelpunt $M_1$ van $c_1$ ligt dus op de bissectrice van $\angle APS$ die immers gelijk is aan de middelloodlijn van $AS$.
Evenzo ligt het middelpunt $M_2$ van $c_2$ op de bissectrice van $\angle BPS$.

Dit betekent dat $\angle M_1PM_2 = \frac 12 \angle APB = 90^\circ$. Dus $P$ ligt volgens Thales op de cirkel met diameter $M_1M_2$.

Met vriendelijke groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 5 november 2018