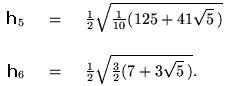WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Oppervlakte en inhoud van een voetbal

Dit is een reactie op vraag 8506

Bedankt voor de site! Toch kom ik er niet uit.. zo geven ze een aantal gegevens waarvan ik niet weet waar ze vandaan komen.. ik heb het ook met mijn wiskundeleraar besproken en die komt er ook niet uit!
Zouden jullie misschien iets meer kunnen uitleggen over de formules die ze geven op de site? Hoe komen ze bijvoorbeeld aan 9/2 en 1/109 in de eerste formule?
Ik hoop dat jullie een antwoord erop weten!
Weer heel erg bedankt!
Karin
Leerling bovenbouw havo-vwo - maandag 17 maart 2003

Antwoord

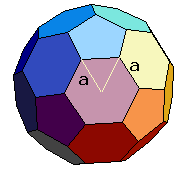Het lichaam bestaat uit 20 piramides met een regelmatige zeshoek als grondvlak en uit 12 piramides met een regelmatige vijfhoek als grondvlak. De totale inhoud is gelijk aan de totale som van inhoud van deze 32 piramides.

Om de inhoud van één zo'n piramide te berekenen heb je de oppervlakte van het grondvlak nodig en de hoogte van de piramide. We nemen voor de ribben van de voetbal de lengte 1.

De oppervlakten van de vijf- en zeshoek kan je vinden op http://mathworld.wolfram.com/RegularPolygon.html

O(zeshoek)=³/₂√3
O(vijfhoek)=¹/₄√(25+10√5)

(Zodat we de oppervlakte van het hele ding al kennen:
O(voetbal)=20·³/₂√3 + 12·¹/₄√(25+10√5)=...)

Nu nog de hoogte van beide piramides, maar dat mag je eerst (weer) zelf proberen. Eenvoudig is het niet..., maar de antwoorden zijn:

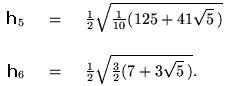
Als je er niet uitkomt kan je wiskundeleraar je misschien een beetje op weg helpen.
HINT: het ding heet 'afgeknotte icosaeder', kan je van een icosaeder makkelijker de inhoud uitrekenen? Zo ja, kan je van de 'dingen' die je er af haalt misschien ook makkelijk de inhoud uitrekenen!? Zie bijvoorbeeld Dodecahedron Measures (onderaan de pagina!)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 24 maart 2003