WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Cirkelverdeling

Mijn tekencursisten maken mandala's. Ik wil ze daarvoor graag een compacte nederlandse uitleg geven van de verschillende cirkelindelingen met passer en liniaal. De cirkel in 3-4-5-6-8-9-12 etc. Kunnen jullie helpen?
Alvast bedankt.
LH
Docent - maandag 17 maart 2003

Antwoord

Beste LH,

De deling van de cirkel in drieën kan als volgt:

Laat AB de diameter van een cirkel met middelpunt C zijn. Teken de cirkel met middelpunt B door C. Deze cirkel snijdt de oorspronkelijke cirkel in de punten D en E. Nu verdelen A, D en E de cirkel in drie gelijke delen.

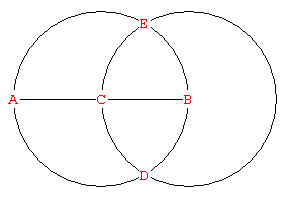
De deling van de cirkel in vieren kan als volgt:

Laat AB weer de diameter van een cirkel zijn met middelpunt C. Nu tekenen we de cirkels met middelpunt A door B en met middelpunt B door A. Deze twee cirkels snijden elkaar in punten D en E. Snijdt nu de lijn DE met de oorspronkelijke cirkel. We krijgen de punten F en G. Nu dlen A, F, B en G de cirkel in vier gelijke delen.

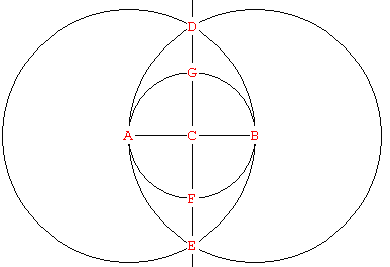
Voor de verdeling van de cirkel in vijf gelijke delen verwijs ik naar een eerder antwoord op Vraag 168.

Hoe nu een verdeling van de cirkel in zestienen maken? Wel, dat kan door de verdeling in vieren tweemaal te 'verdubbelen'. En verdubbelen kan met behulp van bissectrices (deellijnen).
We kunnen telkens bissectrices tekenen van de hoeken die gemaakt worden met het middelpunt. Bijvoorbeeld in het geval van het bovenstaande figuur van de vierdeling, moeten we de bissectrices nemen van $\angle$ACF, $\angle$FCB, $\angle$BCG en $\angle$GCA. Deze snijden de cirkel in vier nieuwe punten, en samen met A, F, B en G delen die de cirkel in achten.

Zie Vraag 8267 voor een beschrijving van de constructie van een bissectrice, en ook onderstaande link naar Ask Dr. Math.

Ik hoop dat dit geholpen heeft!

Zie Geometry Constructions with Compass and Straightedge

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 18 maart 2003