|
|
|
\require{AMSmath}



Hoeken in de ruimte

ABCD is een vierkant met zijden 12 cm. [TM] staat loodrecht op het grondvlak van de piramide en is 15 cm lang. Bereken de hoek B van driehoek BTM.
Kenza
Overige TSO-BSO - maandag 21 mei 2018
Antwoord
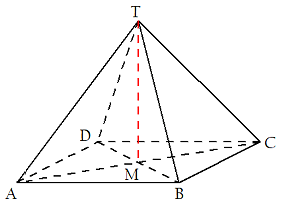
Je wilt $\angle BTM$ berekenen. Je zult dan in $\Delta BTM$ één van de goniometrische verhoudingen sinus, cosinus of tangens moeten gebruiken.
$TM$ weet je, er geldt $TM=15$.
Nu zou ik graag $MB$ ook willen weten. Zou je die uit kunnen rekenen? Als je in het grondvlak kijkt zou dat geen probleem mogen zijn. Een vierkant van 12x12 en dan de helft van de diagonaal? Dat moet kunnen!
Maar dan ben je ook al bijna:
$
\eqalign{\tan \angle BTM = \frac{{TM}}
{{MB}}}
$
...en dan invullen wat je weer en dan ben je er... Zou dat lukken?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 21 mei 2018
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











