WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Brandpunt parabool

Dit is een reactie op vraag 86135

Beste, ik dacht dat ik het begrepen had, maar blijkbaar niet
Als ik het vergelijk met de formules
(x-x₀)²=2p(y-y₀) met brandpunt (x₀,y₀-p)
dan is in de vorige oefening p =-2 en wordt F(-3/2;33/16+2)?
Is dit wel correct?
Vannes
3de graad ASO - dinsdag 8 mei 2018

Antwoord

Nee dat klopt niet. Ik denk dat je formule niet klopt. Op Brandpunt en richtlijn van een parabool gebruik ik iets anders. Zoek de verschillen!:-)

Je krijgt:

$
\eqalign{
& x^2 + 4y = 6 - 3x \cr
& x^2 + 3x = - 4y + 6 \cr
& \left( {x + \frac{3}
{2}} \right)^2 - 2\frac{1}
{4} = - 4y + 6 \cr
& \left( {x + \frac{3}
{2}} \right)^2 = - 4y + \frac{{33}}
{{4}} \cr
& \left( {x + \frac{3}
{2}} \right)^2 = - 4\left( {y - \frac{{33}}
{{16}}} \right) \cr}
$

Dus $p=-1$.

$
\eqalign{
& Top\left( { - \frac{3}
{2},\frac{{33}}
{{16}}} \right) \cr
& F\left( { - \frac{3}
{2},\frac{{17}}
{{16}}} \right) \cr
& r:y = \frac{{49}}
{{16}} \cr}
$

Bewijs

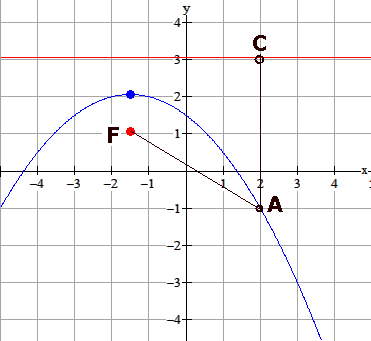
Kies een willekeurig punt $A$ op de parabool. Er geldt:

$
\eqalign{
& A\left( {p, - \frac{{p^2 + 3p - 6}}
{4}} \right),\,\,\,F\left( { - \frac{3}
{2},\frac{{17}}
{{16}}} \right)\,\,\,en\,\,\,C\left( {p,\frac{{49}}
{{16}}} \right) \cr
& d\left( {A,F} \right) = \sqrt {\left( {p - - \frac{3}
{2}} \right)^2 + \left( { - \frac{{p^2 + 3p - 6}}
{4} - \frac{{17}}
{{16}}} \right)^2 } = \frac{{4p^2 + 12p + 25}}
{{16}} \cr
& d\left( {A,C} \right) = \sqrt {\left( {p - p} \right)^2 + \left( { - \frac{{p^2 + 3p - 6}}
{4} - \frac{{49}}
{{16}}} \right)^2 } = \frac{{4p^2 + 12p + 25}}
{{16}} \cr
& d\left( {A,F} \right) = d\left( {A,C} \right) \cr}
$

Helpt dat?
Geogebra
Naschrift
Ik heb 't een en 't ander op De parabool als conflictlijn 2 nog 's uitgewerkt. Je moet maar 's kijken...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 8 mei 2018