|
|
|
\require{AMSmath}



Bewijs
Ik heb een verschrikkelijk moeilijke vraag gekregen:
Door de hoekpunten b en d van een parallellogram abcd trekt men twee evenwijdige rechten X en Y die de diagonaal [ac] snijden in p en q.
Bewijs: ap = qc bp = qd
Ik denk dat dit het gemakkelijkst is met homothetiën of congruente driehoeken.
Zou iemand mij kunnen helpen???
Rob
Rob
2de graad ASO - zaterdag 15 maart 2003
Antwoord
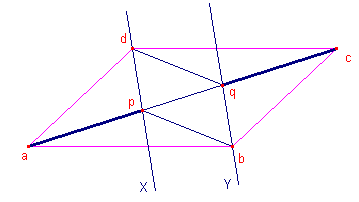
Moeilijk? Je geeft zelf al aan dat je aan congruentie denkt. Je was dus al een klein beetje op weg...
Kijk eens naar de driehoeken apd en cqb.
Van deze driehoeken weet je:
(1) ... ad = bc (waarom?)
(2) ... hoek a = hoek c (waarom?)
(3) ... hoek p = hoek q (waarom?)
Dus (congruentie?) ...
Kijk met de wetenschap die je hierboven hebt verkregen, ook eens naar de driehoeken apb en cqd.
Er zijn nu vast wel drie stel elementen te vinden die gelijk zijn (je hebt al een stel).
En de rest kan je hoop ik zelf wel aanvullen.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 15 maart 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|










