|
|
|
\require{AMSmath}



Substitutiemethode
Goedemorgen,
Vandaag ben ik bezig met het onderwerp substitueren. Ik snap het begin, maar de uitwerking gaat vaak mis. Bij de volgende twee kom ik er dan ook niet echt uit;
a. integraal exsin(ex)dx
b integraal xe-x2/2dx
Ik heb het tijdens college net iets anders uitgelegd gekregen dan dat het in het boek staat (net als op jullie website) en ik kom er nu niet helemaal uit. Hieronder een voorbeeld van hoe het in college is uitgelegd:
integraal x/√1-x2
porbeer: u(x) = 1-x2
u'(x) = -2x $\to$ du/dx = -2x $\to$
du=-2xdx
-1/2 du = xdx
vul nu in:-1/2 du/√u
-1/2 $\int{}$ du/√u
-1/2 $\int{}$ 1/√udu
-1/2 $\int{}$ u-1/2du
- -1/2 2u1/2 (ik snap niet helemaal waar deze
en de volgende stap vandaan komt?)
$\int{}$1u-1/2du=2u1/2
Hoe kom je van hier nu naar -√1-x2
controleren: -√1-x2 = - (1-x2)1/2
F'(x) = -1/2(1-x2)-1/2(-2x)
x(1-x2)-1/2 = x/√1-x2
Hopelijk kunnen jullie me hiermee verder helpen. Alvast bedankt voor de moeite!
Bo
Student universiteit - donderdag 14 december 2017
Antwoord
Hallo Bo,
In het uitgewerke voorbeeld staat inderdaad een schrijffout. Het gaat goed tot:
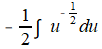
Ik laat nu de integratieconstante even buiten beschouwing. Je weet dan:
f(x)=x-1/2 geeft na primitiveren: F(x)=2x1/2
(Controleer dit door F(x) weer te differentiŽren)
Dus:
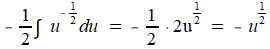
Terug-substitueren levert dan F(x)=-√(1-x2)
Dan jouw vraag a. Dat gaat op dezelfde manier:
Probeer u=ex
Dat geeft:
du/dx=ex
ofwel:
dx = 1/ex∑du
Vul deze uitdrukking van dx nu in je functie in:
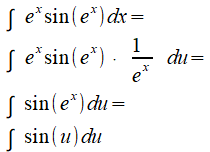
Het is een kwestie van zorgvuldig noteren 
Vraag b gaat op dezelfde manier:
- Kies u=x2/2
- Bepaal du/dx
- Vorm dit om tot dx = ......
- Vervang dx in je oorspronkelijke functie door wat je bij de vorige stap hebt gevonden
- Uiteraard vervang je x2/2 door u
- Je kunt je oorspronkelijke functie nu aanzienlijk vereenvoudigen.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 14 december 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








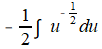
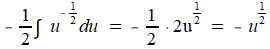
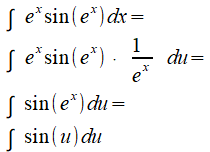



 Re: Substitutiemethode
Re: Substitutiemethode