|
|
|
\require{AMSmath}
Berekening diagonaal willekeurige vierhoek
Van een (iets) onregelmatige vierhoek is de lengte van alle 4 zijden bekend. Deze liggen dicht bij elkaar maar zijn toch allemaal verschillend; de een wat meer dan de ander. Er zijn geen hoeken bekend maar de oppervlakte wel. Hoe kan ik een van de diagonalen berekenen? (maakt niet uit welke) Persoonlijk zat ik voor een oplossing te denken aan een combinatie van de formule van Heron en 'vergelijkingen'.
Kazimi
Student hbo - zondag 13 augustus 2017
Antwoord
Hallo Kazimier,
Goed plan: de formule van Heron voor een driehoek met zijden a, b en c is te schrijven in deze vorm (zie Wikipedia: Formule van Heron):
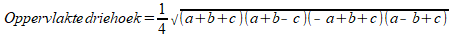
Dit kan je twee keer toepassen bij jouw vierhoek met bekende zijden p, q, r en s. Teken een diagonaal d waardoor twee driehoeken ontstaan:
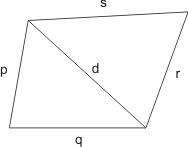
De oppervlakte A van de vierhoek is de som van de oppervlaktes van de twee driehoeken (ik laat figuren met daarin een hoek groter dan 180 graden even buiten beschouwing):
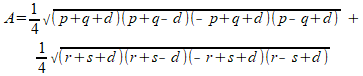
Hierin is de lengte d de enige onbekende.
De vergelijking lijkt me alleen numeriek oplosbaar. Onder beide wortels staat 4e-graads uitdrukking in d, je kunt dus meerdere oplossingen verwachten. Dat is te begrijpen, zie de figuur hieronder:
 
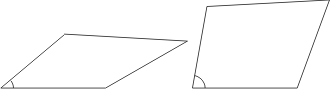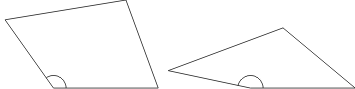
Je ziet vier keer een vierhoek met steeds dezelfde zijden. Wanneer de hoek tussen de zijden links onder toeneemt, neemt de oppervlakte aanvankelijk ook toe en later weer af. Een gegeven oppervlakte (niet de maximaal mogelijke waarde) kom je dus twee keer tegen, bij twee verschillende vierhoeken.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 14 augustus 2017
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
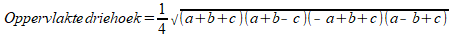
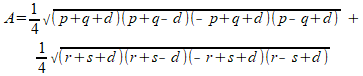
Re: Berekening diagonaal willekeurige vierhoek