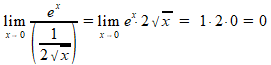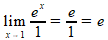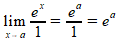WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Limieten van e functies

Dit is een reactie op vraag 84865

Ik heb deze methode al gegoogled maar ook hiermee kom ik er niet uit.

(e^x - 1) / √x = e^x / 1/2 x^-1/2
Geeft noemer nul bij x = 0
Teller = e^x = 1 + 0 = 1
Waar antwoord: 0

De tweede geeft:
e^x / x =
2 / 1
Waar het antwoord: e

De derde geeft:
0 / 0
waar antwoord e^a
Kevin
Student hbo - vrijdag 4 augustus 2017

Antwoord

Hallo Kevin,

Het differentiëren en vervolgens invullen moet je wel zorgvuldig uitvoeren. Steeds is sprake van een functie f(x) = ^g(x)/_h(x) waarbij g(x) en h(x) naar 0 gaan. We berekenen dus de limiet van ^g`(x)/_h`(x):

Opgave 1:
g(x)=e^x-1, dus g'(x)=e^x
h(x)=√x, dus h'(x)=¹/₂·x^-¹/₂x = ¹/_(2√x)

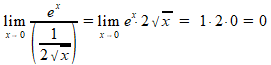
Opgave 2:
g(x)=e^x-e, dus g'(x)=e^x
h(x)=x-1, dus h'(x)=1

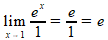
Opgave 3:
g(x)=e^x-e^a, dus g'(x)=e^x
h(x)=x-a, dus h'(x)=1

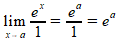
OK zo?

PS: Bedenk dat de eerste functie alleen bestaat voor x groter of gelijk aan nul. Strikt genomen bestaat 'de' limiet voor x naar 0 dan niet, alleen de rechterlimiet voor x naar nul bestaat.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 4 augustus 2017