WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Constructie cirkel die raakt aan vaste cirkel en 2 andere orthogonaal snijdt

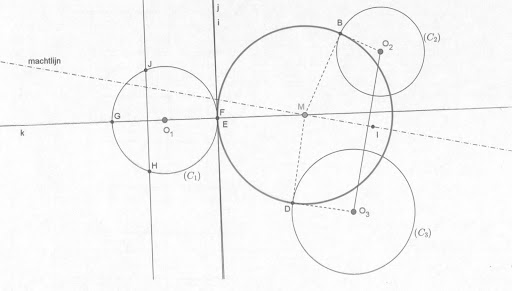
Opgave: Gegeven zijn drie vaste cirkels (C1), (C2), (C3) die elkaar niet snijden. Bepaal dan een cirkel die (C1) raakt en (C2) resp. (C3) orthogonaal snijdt.

Voorlopige stand van zaken: Daar de cirkel (C1) uitwendig resp. inwendig kan raken aan de gezochte cirkel, is het zeker dat er 2 oplossingen zullen zijn. Daar de machtlijn van 2 cirkels de meetkundige plaats is van de middelpunten van de cirkels, die (C2) en (C3) orthogonaal snijden, kunnen we al aannemen dat het middelpunt van de gezochte cirkels op die machtlijn moeten liggen.

Het probleem is de juiste positie vinden op die machtlijn:

Ik probeerde via een inversie, maar dat lukte tot hiertoe niet. Ofwel is een inversie niet de juiste keuze ofwel koos ik niet het juiste inversiecentrum (ik koos o.a. het punt G, H, F en J).

VRAAG: Kunnen jullie mij een tip bezorgen, om de juiste positie van M op de machtlijn te achterhalen?

Van harte bedankt voor jullie eventuele tussenkomst!
Yves D
Iets anders - maandag 31 juli 2017

Antwoord

Hallo Yves,

Mijn tip is:
De cirkels die $(C_2)$ en $(C_3)$ orthogonaal snijden hebben niet alleen hun middelpunt $M$ op de machtlijn, maar tevens gaan ze door twee vaste punten op $O_2O_3$. Daarmee reduceert het probleem tot een cirkel door twee gegeven punten die raakt aan $(C_1)$.

Succes.

Met vriendelijke groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 4 augustus 2017