|
|
|
\require{AMSmath}



Kaarten verdelen
Ik heb een vraag die betrekking heeft op een kaartspel.
De vraag houdt me al enige tijd bezig en ik kom er niet uit.
Stel:
We spelen met een compleet dek kaarten (52 kaarten) en iedereen krijgt 13 kaarten. Ik heb zelf 6 hartenkaarten gekregen.
Wat is dan de kans dat een van de drie tegenspelers 5 hartenkaarten of meer vast heeft?
volgens mij is er een analogie met de volgende vraag en is de vraag op te lossen met herhalingscombinaties: Verdelen onder deelnemers
Volgens mij mag er aangenomen worden dat er 7 hartenkaarten te verdelen zijn over 3 personen (de rest van de kaarten interesseert me niet).
Totaal aantal combinaties:
7 keer kiezen uit 3 personen = ((3-1)+7) boven 7 = (9 boven 7) = 36 combinaties
Totaal aantal combinaties, waarbij 1 persoon 5 hartenkaarten krijgt en de overige 2 kaarten willekeurig worden verdeeld:
2 keer kiezen uit 3 personen = ((3-1)+2) boven 2 = (4 boven 2) = 6 combinaties
(Dat zou dan zijn:
7 / 0 / 0
6 / 1 / 0
6 / 0 / 1
5 / 2 / 0
5 / 0 / 2
5 / 1 / 1)
Kans op 5 hartenkaarten bij 1 speler = 6 /36 ????
Ben ik warm of sla ik de plank volledig mis??
Thijs
Iets anders - dinsdag 25 juli 2017
Antwoord
Hallo Thijs,
Deze vraag is niet zomaar met herhalingscombinaties te beantwoorden. Immers, bij die aanpak verdeel je denkbeeldig de resterende hartenkaarten over 3 tegenspelers waarbij elke tegenspeler steeds dezelfde kans heeft dat hij de volgende hartenkaart krijgt. Maar dit is onjuist: een hartenkaart wordt willekeurig verdeeld over de 'nog open plekken'. Een tegenspeler die al veel hartenkaarten heeft, heeft minder kans op de volgende hartenkaart dan een speler die nog maar weinig hartenkaarten heeft. De kans op elke combinatie is dus niet constant, je mag dus niet de kansregel van Laplace toepassen.
De volgende aanpak lijkt mij beter:
Eerst geven we onszelf 6 hartenkaarten en 7 overige kaarten. Dit is de uitgangspositie.
Vervolgens geven we de eerste tegenspeler 13 kaarten, we berekenen de kans dat hij minimaal 5 hartenkaarten krijgt, dus 5 harten en 8 andere kaarten, 6 harten en 7 andere, of 7 harten en 6 andere:
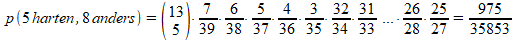
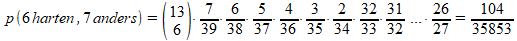
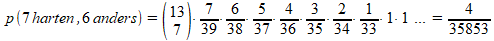
De kans dat de eerste tegenspeler minimaal 5 hartenkaarten heeft, is de som van deze kansen:
p(tegenspeler 1 heeft minimaal 5 harten) = 1083/35853 = 19/629
De overige twee tegenspelers hebben dezelfde kans, dus de kans dat één van de tegenspelers minimaal 5 harten heeft, is drie keer zo groot:
p(een van de tegenspelers heeft minimaal 5 harten) = 3·19/629 = 57/629  0,09. 0,09.
Nu maar hopen dat ik geen rekenfout heb gemaakt 

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 25 juli 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








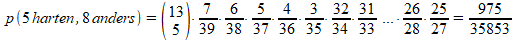
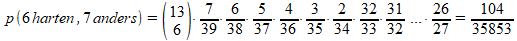
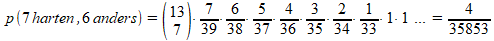
 0,09.
0,09. 


 Re: Kaarten verdelen
Re: Kaarten verdelen